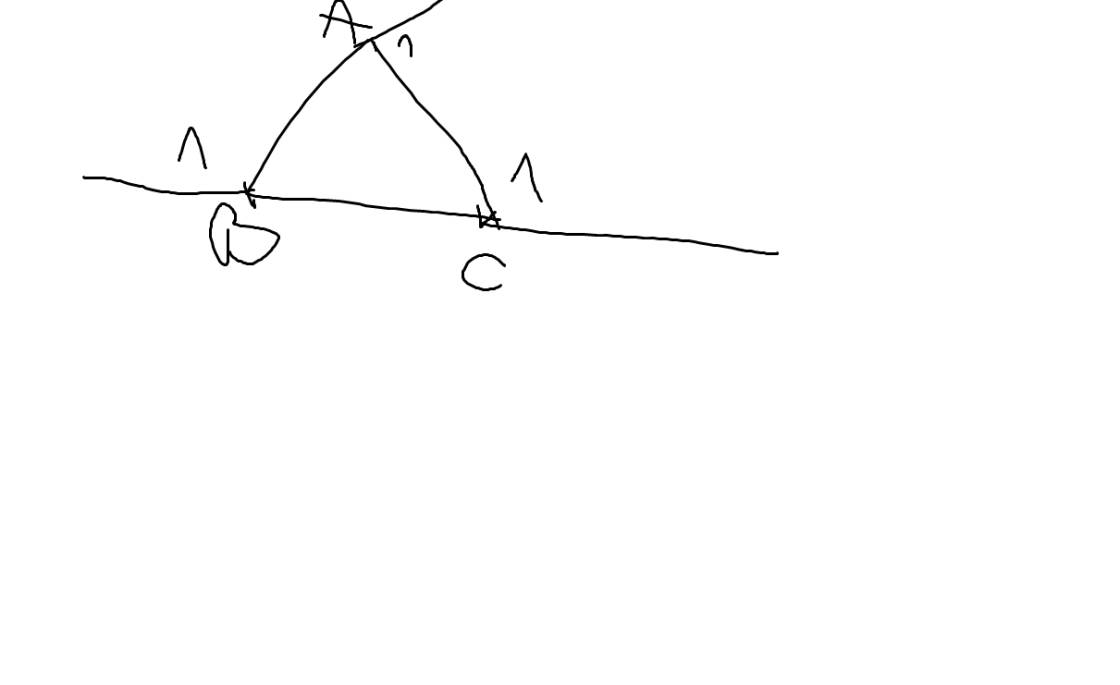
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-\widehat{ABC}\)
\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{C_1}=180^0-\widehat{ACB}\)
\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)
=>\(\widehat{A_1}=180^0-\widehat{BAC}\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)
\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)
\(=540^0-180^0=360^0\)














