Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng?
A. ln (ab) = ln a + ln b
B. ln a b = ln a ln b
C.ln(ab)=lna.lnb
D. ln a b = ln a - ln b
Gọi ∫ 1 3 1 x - 5 2 x + 2 d x = a + ln b với a, b là số thực. Mệnh đề nào dưới đây đúng?
A. a b = 8 81 .
B. a + b = 7 24 .
C. a b = 9 8 .
D. a + b = 3 10 .
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:

Cho a = l o g 3 , b = l n 3. Mệnh đề nào sau đây đúng
A. a b = e 10
B. 10 a = e b
C. 1 a + 1 b = 1 10 e
D. 10 b = e a
Gọi a là số thực lớn nhất để bất phương trình x 2 - x + 2 + a ln ( x 2 - x + 1 ) ≥ 0 nghiệm đúng với mọi x. Mệnh đề nào sau đây đúng?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đáp án B
Đặt 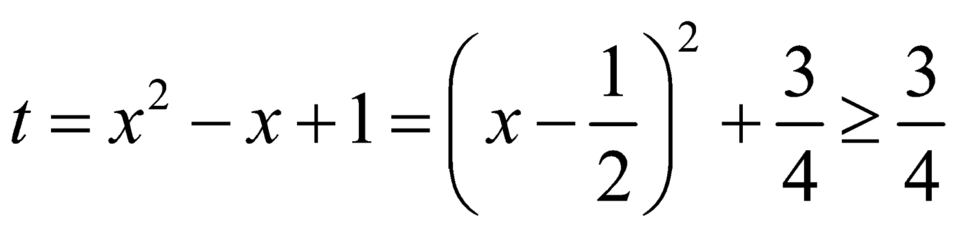
Ta có:
![]()
![]()
Đặt ![]() .
.
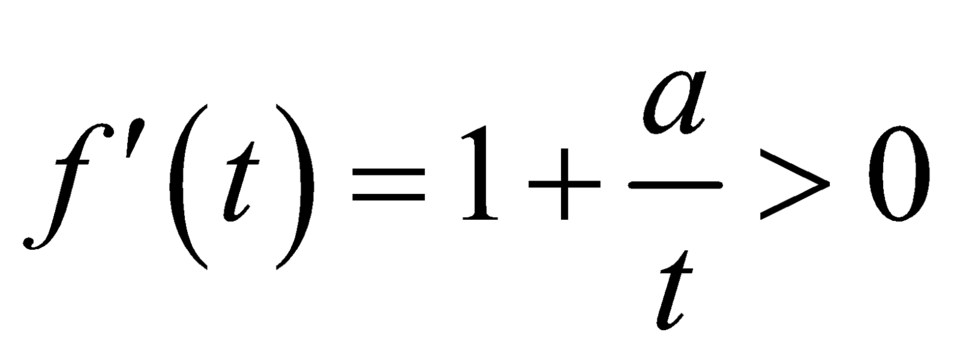
![]() là hàm số đồng biến trên
là hàm số đồng biến trên 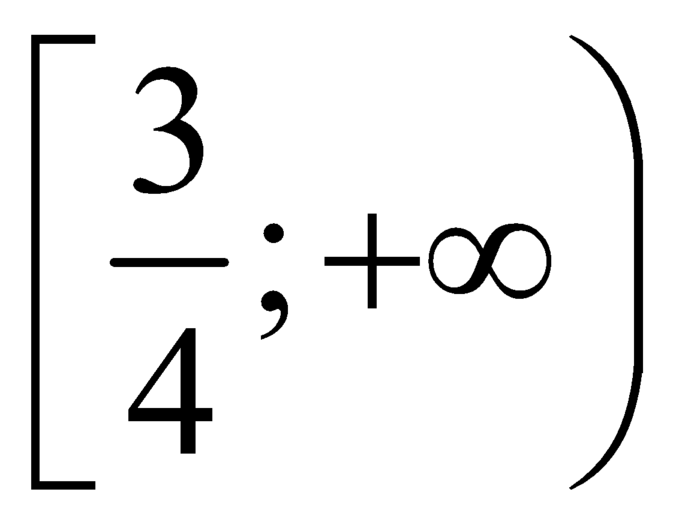 .
.
Khi đó 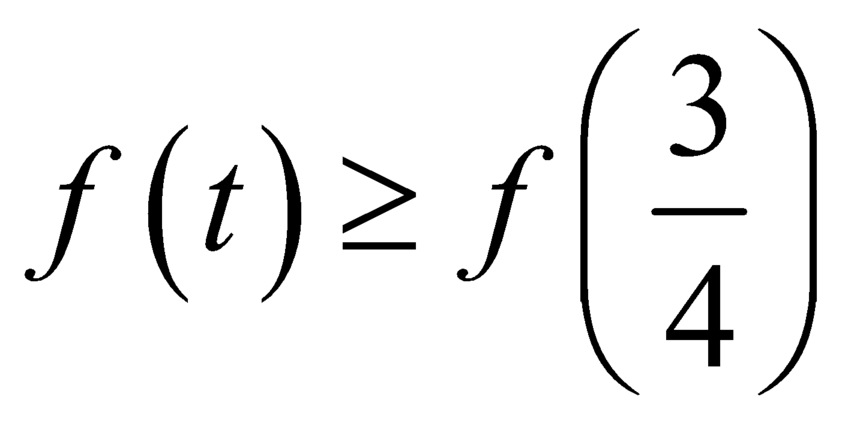
![]()
![]()
![]()
Cho số thực dương k > 0 thỏa ∫ 0 2 d x x 2 + k = ln 2 + 5 . Mệnh đề nào sau đây đúng?
A. k > 3 2
B. 0 < k ≤ 1 2
C. 1 2 < k ≤ 1
D. 1 < k ≤ 3 2
Cho số thực dương k > 0 thỏa mãn ∫ 0 2 d x x 2 + k = ln ( 2 + 5 ) . Mệnh đề nào sau đây đúng?
![]()
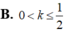
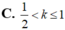
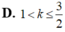
Cho ∫ ln 2 ln 3 1 x + 3 d x = ln ( a . log b c ) . Mệnh đề nào dưới đây đúng?
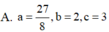
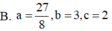
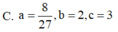
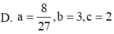
Cho ∫ ln 2 ln 3 ( 1 x + 3 ) d x = ln ( a log b c ) . Mệnh đề nào dưới đây đúng?
A. a = 27 8 , b = 2 , c = 3
B. D.
C. a = 8 27 , b = 2 , c = 3
D. a = 8 27 , b = 3 , c = 2
Cho ∫ ln 2 ln 3 ( 1 x + 3 ) d x = ln ( a log b c ) Mệnh đề nào dưới đây đúng?
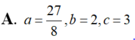
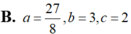
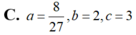
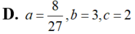
Hàm số f ( x ) = ln ( e x + m ) có f ' ( - ln 2 ) = 3 2 .Mệnh đề nào dưới đây đúng?
A. m ∈ - 2 ; 0
B. m ∈ - 5 ; - 2
C. m ∈ 1 ; 3
D. m ∈ 0 ; 1
Có
f ' x = e x e x + m ⇒ f ' - ln 2 = 3 2 ⇔ e - ln 2 e - ln 2 + m = 3 2 ⇔ m = - 1 6 .
Chọn đáp án A.