Cho hàm số y=f(x) , có đồ thị hàm số y=f'(x) có bảng xét dấu sau:
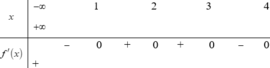
Hàm số y = 3 f ( x + 2 ) - x 3 + 3 x đồng biến trên khoảng nào dưới đây?
A. ( 1 ; + ∞ )
B. ( - ∞ ; - 1 )
C. (0;2)
D. (-1;0)
Cho hàm số y=f(x) xác định trên R và có bảng xét dấu đạo hàm như sau:

Khi đó số điểm cực trị của đồ thị hàm số y=f(x) là
A. 3
B. 2
C. 4
D. 1
Chọn A.
Tại các điểm x 1 , x 2 , x 3 hàm số y=f(x) xác định và hàm số y=f’(x) không xác định hoặc bằng 0, ngoài ra hàm số y=f’(x) còn đổi dấu qua các điểm đó nên hàm số y=f(x) có 3 điểm cực trị.
Cho hàm số \(y=f\left(x\right)\) là hàm số bậc bốn thỏa mãn \(f\left(0\right)=0\) .Hàm số \(y=f'\left(x\right)\) có bảng biến thiên như sau:
Hàm số \(g\left(x\right)=\left|f\left(x^2\right)-x^2\right|\) có bao nhiêu điểm cực trị?
A.1
B.3
C.5
D.7
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
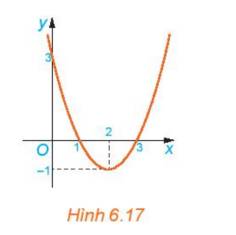
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
Cho hàm số f(x) có f ( 2 ) = f ( - 2 ) = 0 và có bảng xét dấu của đạo hàm như sau:

Hàm số y = ( f ( 3 - x ) ) 2 nghịch biến trên khoảng nào dưới đây?
A. (2;5).
B. (1;+∞).
C. (-2;-1).
D. (1;2).
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng xét dấu như sau:
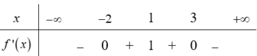
Hàm số y= f ( x 2 + 2 x ) nghịch biến trên khoảng nào dưới đây?
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) có đạo hàm trên R và có đồ thị của hàm số y = f'(x) như hình vẽ. Xét hàm số g(x) = f x 2 - 2
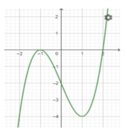
Mệnh đề nào sau đây sai?
A. Hàm số g(x) nghịch biến trên (0;2)
B. Hàm số g(x) đồng biến trên (2;+ ∞ )
C. Hàm số g(x) nghịch biến trên (- ∞ ;-2)
D. Hàm số g(x) nghịch biến trên (-1;0).
Chọn D.
Xét g(x) = f x 2 - 2
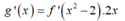
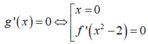
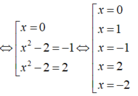
Bảng xét dấu g’(x):

Suy ra hàm số g(x) nghịch biến trên (-1;0) là sai.
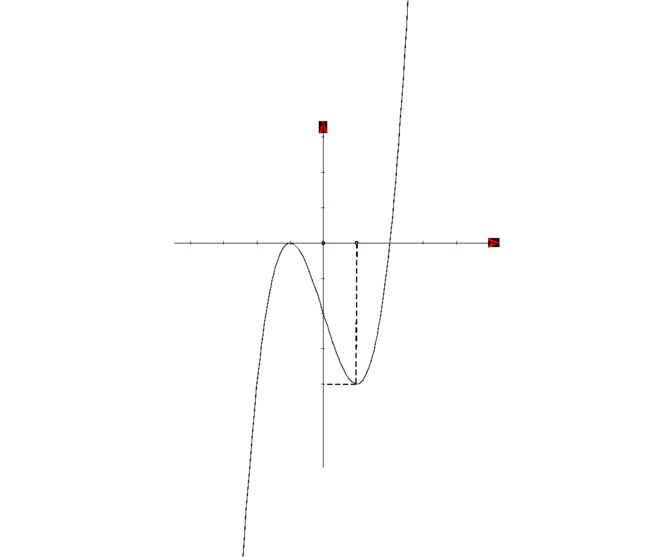
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm y=f '(x) như hình vẽ. xét hàm số g(x)=f(2-x^2). Mệnh đề nào dưới đây sai?
A. Hàm số ![]() đạt cực trị tại
đạt cực trị tại ![]() .
.
B. Hàm số ![]() nghịch biến trên
nghịch biến trên ![]() .
.
C. Hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
D. Hàm số ![]() đồng biến trên
đồng biến trên ![]() .
.
Cho hàm số y=f(x) liên tục trên ℝ và có bảng xét dấu f’(x) như sau
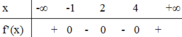
Hàm số y=f(x) có bao nhiêu điểm cực trị?
A. 1.
B. 2.
C. 3.
D. 0.
Cho hàm số y= f(x) liên tục trên R và có bảng xét dấu f’(x) như sau
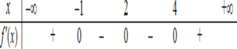
Hàm số y= f(x) có bao nhiêu điểm cực trị?
A. 1.
B. 2.
C. 3.
D. 0.