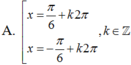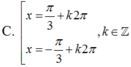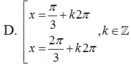Nghiệm của phương trình 2cos2x + 2cosx
-
2
0
Đọc tiếp
Nghiệm của phương trình 2cos2x + 2cosx - 2 = 0
Những câu hỏi liên quan
Tổng các nghiệm thuộc khoảng
0
;
3
π
của phương trình
sin
2
x
-
2
cos
2
x
+
2
sin
x
2
cos
x
+
4
là A. 3
π
B.
π
C. 2
π
D.
π
2
Đọc tiếp
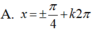
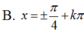
Tổng các nghiệm thuộc khoảng 0 ; 3 π của phương trình sin 2 x - 2 cos 2 x + 2 sin x = 2 cos x + 4 là
A. 3 π
B. π
C. 2 π
D. π 2
1) phương trình cosx = m có nghiệm khi
2) nghiệm của phương trình \(tan2x-1=0\) là
3) nghiệm của phương trình \(2cos2x=-2\)
Giải phương trình:
a, 2sin2x - cos2x = 7sinx + 2cosx - 4
b, sin2x - cos2x + 3sinx - cosx -1 = 0
c, sin2x - 2cos2x + 3sinx - 4cosx + 1 = 0
a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)
Nghiệm của phương trình 2cos2x + 1 = 0 là:
Nghiệm của phương trình
2
cos
2
x
+
9
sin
x
-
7
0
là: A.
x
-
π
2
+
k
2
π
,
k
∈
Z
B.
x
-
π
2
+
k
π
,
k
∈
Z
C. ...
Đọc tiếp
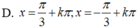
Nghiệm của phương trình 2 cos 2 x + 9 sin x - 7 = 0 là:
A. x = - π 2 + k 2 π , k ∈ Z
B. x = - π 2 + k π , k ∈ Z
C. x = π 2 + k π , k ∈ Z
D. x = π 2 + k 2 π , k ∈ Z
Tập nghiệm của phương trình 2cos2x+10 là A.
S
π
3
+
k
2
π
,
-
π
3
+
k
2...
Đọc tiếp
Tập nghiệm của phương trình 2cos2x+1=0 là
A. S = π 3 + k 2 π , - π 3 + k 2 π , k ∈ Z .
B. S = 2 π 3 + k 2 π , - 2 π 3 + k 2 π , k ∈ Z .
C. S = π 3 + k π , - π 3 + k π , k ∈ Z .
D. S = π 6 + k π , - π 6 + k π , k ∈ Z .
Tập nghiệm của phương trình
2
cos
2
x
+
1
0
là A.
S
π
3
+
k
2
π
,
-
π
3
+
k
2
π...
Đọc tiếp
Tập nghiệm của phương trình 2 cos 2 x + 1 = 0 là
A. S = π 3 + k 2 π , - π 3 + k 2 π , k ∈ ℤ
B. S = 2 π 3 + k 2 π , - 2 π 3 + k 2 π , k ∈ ℤ
C. S = π 3 + k π , - π 3 + kπ , k ∈ ℤ
D. S = π 6 + k 2 π , - π 6 + k 2 π , k ∈ ℤ
Nghiệm của phương trình
5
-
5
sin
x
+
2
cos
2
x
0
là A. kπ, k ϵ ℤ B. k2π, k ϵ ℤ C.
π
2
+
k
2
π
,
k
∈
ℤ
D.
π
6
+
k
2
π
,
k
∈
ℤ
Đọc tiếp
Nghiệm của phương trình 5 - 5 sin x + 2 cos 2 x = 0 là
A. kπ, k ϵ ℤ
B. k2π, k ϵ ℤ
C. π 2 + k 2 π , k ∈ ℤ
D. π 6 + k 2 π , k ∈ ℤ
Nghiệm của phương trình 1 – 5sinx + 2cos2x 0 là
Đọc tiếp
Nghiệm của phương trình 1 – 5sinx + 2cos2x =0 là
