Đáp án B

Hàm số xác định với mọi  x ∈ ( 1 ; 2 ) ⇔ − x 2 + m x + 2 m + 1 > 0 ∀ x ∈ 1 ; 2

⇔ m x + 2 > x 2 − 1 ∀ x ∈ 1 ; 2 ⇔ m > x 2 − 1 x + 2 ∀ x ∈ 1 ; 2 ⇔ m > M a x 1 ; 2 g x

Xét g x = x 2 − 1 x + 2  với x ∈ 1 ; 2 ta có

g x = x 2 − 1 x + 2 = x − 2 + 3 x + 2 ⇒ g ' x = 1 − 3 x + 2 2 > 0 ∀ x ∈ 1 ; 2

Do đó g x  đồng biến trên khoảng 1 ; 2 ⇒ m ≥ g 2 = 3 4  là giá trị cần tìm

Đáp án B

Hàm số xác định với mọi  x ∈ 1 ; 2 ⇔ − x 2 + m x + 2 m + 1 > 0 ∀ x ∈ 1 ; 2 .

⇔ m > x 2 − 1 x + 2 = g x ∀ x ∈ 1 ; 2 ⇔ m > M ax 1 ; 2 g x

Xét  g x = x 2 − 1 x + 2 = x − 2 + 3 x + 2 ⇒ g ' x = 1 − 3 x + 2 2 > 0 ∀ x ∈ 1 ; 2

Do đó lim x → 2   f x = 3 4 .  Vậy m ≥ 3 4  là giá trị cần tìm.

Chọn đáp án B

Để y xác định thì \(\left(m-2\right)x+2m-3\ge0\forall x\in\left[-1;4\right]\)

\(\Leftrightarrow mx-2x+2m-3\ge0\)

\(\Leftrightarrow m\left(x+2\right)-2x-3\ge0\)

\(\Leftrightarrow m\ge\dfrac{2x+3}{x+2}\left(x+2>0\forall x\in\left[-1;4\right]\right)\)

\(\Rightarrow1\le m\le\dfrac{11}{6}\)

Chọn D.

Tập xác định: D =  ℝ

Ta có

Xét m = 1, ta có y' = -3 < 0 ∀ x ∈ ℝ  nên nghịch biến trên tập xác định.

Xét m ≠ 1 Để hàm số trên nghịch biến trên tập xác định khi và chỉ khi 

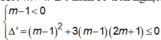
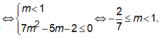
Vậy với  - 2 7 ≤ m ≤ 1 thì hàm số y =  ( m - 1 ) x 3 + ( m - 1 ) x 2 - ( 2 m + 1 ) + 5  nghịch biến trên tập xác định.

Đáp án A