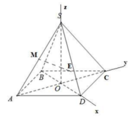
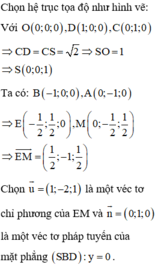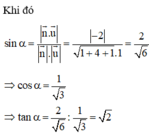Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính góc tạo bởi SA và CD.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính góc tạo bởi SA và CD.
Những câu hỏi liên quan
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính góc tạo bởi SA và CD. A.
30
°
B.
90
°
C.
120
°
D.
60
°
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính góc tạo bởi SA và CD.
A. 30 °
B. 90 °
C. 120 °
D. 60 °
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Cô sin của góc tạo bởi 2 mặt phẳng (SAD) và (SBC) bằng
A. 1 3
B. 1 3
C. 1 6
D. 1 6
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA,
α
là góc tạo bởi đường thẳng EM và mặt phẳng (SBD),
tan
α
bằng: A.
2
.
B.
3
C. 2 D. 1
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 2 .
B. 3
C. 2
D. 1
Đáp án A
Gọi I,J lần lượt là trung điểm cạnh BC và SA
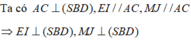
Suy ra, IJ là hình chiếu vuông góc của EM lên (SBD)
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA,
α
là góc tạo bởi đường thẳng EM và mặt phẳng
S
B
D
,
tan
α
bằng A.
2
B.
3
C. 2 D. 1
Đọc tiếp
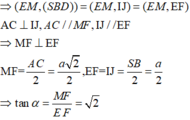
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của các cạnh BC và SA, α là góc tạo bởi đường thẳng EM và mặt phẳng S B D , tan α bằng
A. 2
B. 3
C. 2
D. 1
Đáp án A
Gọi I,J lần lượt là trung điểm cạnh BC và SA
Ta có A C ⊥ S B D , EI // AC, MJ//AC => E I ⊥ ( S B D ) , M J ⊥ ( S B D )
Suy ra, IJ là hình chiếu vuông góc của EM lên (SBD)
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E; M lần lượt là trung điểm của BC và SA. Gọi α là góc tạo bởi EM và (SBD). Khi đó tanα bằng: A. 1. B. 2. C.
2
D.
3
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E; M lần lượt là trung điểm của BC và SA. Gọi α là góc tạo bởi EM và (SBD). Khi đó tanα bằng:
A. 1.
B. 2.
C. 2
D. 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của
B
C
,
S
A
,
α
là góc tạo bởi đường thẳng EM và mặt phẳng (SBD),
tan
α
bằng: A. 1 B. 2 C.
2
D.
3
Đọc tiếp
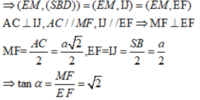
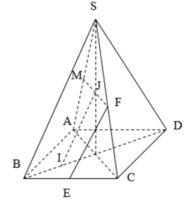
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của B C , S A , α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 1
B. 2
C. 2
D. 3
Cho hình chóp tứ giác đều S.ABCD có tất cả cạnh bằng a (tham khảo hình vẽ bên). Góc giữa hai đường thẳng SA và CD bằng
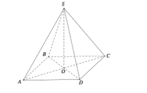
A. 60°.
B. 30°.
C. 45°.
D. 90°.
19 tháng 3 2021 lúc 16:56
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Tính côsin góc giữa đường thẳng SA và mp(ABCD)?
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SAO}\) hay \(\widehat{SAC}\) là góc giữa SA và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(cos\widehat{SAC}=\dfrac{SA^2+AC^2-SC^2}{2SA.AC}=\dfrac{\sqrt{2}}{2}\)
Đúng 2
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi E, M lần lượt là trung điểm của BC, SA, α là góc tạo bởi đường thẳng EM và mặt phẳng (SBD), tan α bằng:
A. 1
B. 2
C. 2
D. 3
Đáp án C
Phương pháp:
- Gắn hệ trục tọa độ Oxyz, tìm tọa độ các điểm E, M.
- Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng: sin α = n → . u → n → . u →
Cách giải:
Đúng 0
Bình luận (0)