Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = 3 a , A D = 4 a , B A D ^ = 120 0 . Cạnh bên SA vuông góc với đáy và S A = 2 a 3 . Tính góc giữa hai mặt phẳng S B C và S C D
A. 45 0
B. arccos 17 2 26
C. 60 °
D. 30 °
Những câu hỏi liên quan
Bài 3 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M, N là trung điểm cạnh SC; SD
a) CMR: MN // (SAB); MM // (ABCD)
b) CMR: MO // (SAB)
Bài 4 :Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, M,N, P là trung điểm cạnh SA, SB, SC.
a) Chứng minh rằng : MN // (SCD).
b) Chứng minh rằng: MO // (SAB)
Giúp vs bạn !!
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt
S
A
→
a
→
,
S
B
→
b
→
,
S
C
→
c
→
,
S
D
→
d
→
....
Đọc tiếp
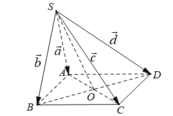
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt S A → = a → , S B → = b → , S C → = c → , S D → = d → . Chứng minh: a → + c → = d → + b → .
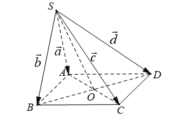
- Gọi O là tâm của hình bình hành ABCD. Ta có:
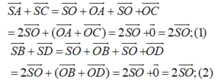
- Từ (1) và (2) suy ra:
Đúng 0
Bình luận (0)
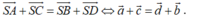
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB = a, SA = a 3 vuông góc với (ABCD). Tính góc giữa hai đường thẳng SB và CD.
A. 60 °
B. 30 °
C. 45 °
D. 90 °
Chọn A.
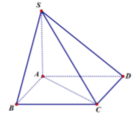
Ta có ABCD là hình bình hành => AB//CD
Do đó (SB,CD) = (SB,AB) = SBA
Vì SA ⊥ (ABCD) => SA ⊥ AB => ∆ SAB vuông tại A.
Xét tam giác vuông SAB ta có: 
Vậy (SB;CD) = 60 °
Đúng 0
Bình luận (0)
Phần I: Trắc nghiệmCho hình chóp S.ABCD có đáy ABCD là hình bình hành. - Đặt
S
A
→
a
→
,
S
B
→
b
→
,
S
C
→
c
→
,
S
D
→
d...
Đọc tiếp
Phần I: Trắc nghiệm
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
- Đặt S A → = a → , S B → = b → , S C → = c → , S D → = d → .Khẳng định nào sau đây đúng?
A. a → + c → = d → + b →
B. a → + b → = d → + c →
C. a → + d → = b → + c →
D. a → + b → + c → + d → = 0 →
Chọn A.
- Gọi O là tâm của hình bình hành ABCD. Ta có:
Đúng 0
Bình luận (0)
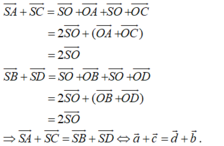
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong mặt phẳng (ABCD) vẽ
đường thẳng d đi qua A và không song song với các cạnh của hình bình hành. Trên cạnh SC lấy
điểm M. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (M,d)
1. cho hình chóp S.ABCD có đáy ABCD là hình vuông. Số mặt bên của hình chóp là? Kể tên2. cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Số cạnh đáy của hình chóp là? Kể tên3. cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Vị trí tương đối giữa 2 đường thẳng SA và BC là4. hình tứ diện ABCD có bao nhiêu đỉnh? Kể tên5. hình chóp S.ABCD có bao nhiêu mặt. Kể tên6. các yếu tố nào sau đây xác định 1 mặt phẳng duy nhấtA. ba điểm phân biệtB. 1 điểm và 1 đường thẳngC. 2 đường thẳng cắt nhauD. 4 đ...
Đọc tiếp
1. cho hình chóp S.ABCD có đáy ABCD là hình vuông. Số mặt bên của hình chóp là? Kể tên
2. cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Số cạnh đáy của hình chóp là? Kể tên
3. cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Vị trí tương đối giữa 2 đường thẳng SA và BC là
4. hình tứ diện ABCD có bao nhiêu đỉnh? Kể tên
5. hình chóp S.ABCD có bao nhiêu mặt. Kể tên
6. các yếu tố nào sau đây xác định 1 mặt phẳng duy nhất
A. ba điểm phân biệt
B. 1 điểm và 1 đường thẳng
C. 2 đường thẳng cắt nhau
D. 4 điểm phân biệt
1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có
S
A
a
,
S
B
2
a
,
S
C
3
a
và
A
S...
Đọc tiếp
Cho hình chóp S.ABCD có S A = a , S B = 2 a , S C = 3 a và A S B ⏜ = A S C ⏜ = B S C ⏜ = 60 o . Biết đáy ABCD là hình bình hành. Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 2
B. V = a 3 2 2
C. V = a 3 2 3
D. V = 3 a 3 2
Chọn đáp án A
Áp dụng công thức
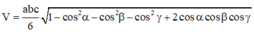
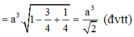
Suy ra V S . A B C D = a 2 2 ( đ v t t )
Đúng 0
Bình luận (0)
1.Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi A',B' lần lượt là trung điểm của SA,SB . Đường thẳng A' B' song song với mặt phẳng nào dưới đây?
A. (SAB).
B. ( ABCD) .
C. (SAD).
D. (SBC).
2.Cho hình hộp ABCD.A' B' C' D' . Mặt phẳng ( ABA') song song với:
A. ( AA'C') .
B. (CC'D').
C. ( ADD').
D. (BB'A').
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh của hình bình hành, d cắt BC tại E. Gọi C’ là một điểm nằm trên cạnh SC.
a) Tìm giao điểm M của CD và mp(C’AE).
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C’AE).
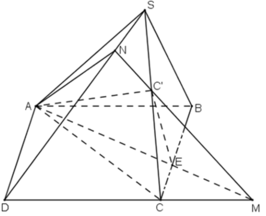
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có SA
⊥
(ABCD), đáy ABCD là hình bình hành có AB
⊥
AC. Biết SA AD a. Tính khoảng cách h từ A tới mặt phẳng (SCD). A. h
a
2
2
B. h
a
3
7
C. h
a
3
2
D. h
a
2
Đọc tiếp
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình bình hành có AB ⊥ AC. Biết SA = AD = a. Tính khoảng cách h từ A tới mặt phẳng (SCD).
A. h = a 2 2
B. h = a 3 7
C. h = a 3 2
D. h = a 2