Cho dãy số ( u n ) bởi công thức truy hồi sau: u 1 = 0 u n + 1 = n + u n ; n ≥ 1 . ; u 218 nhận giá trị nào sau đây?
A. 23653.
B. 46872.
C. 23871.
D. 23436.
Những câu hỏi liên quan
Cho dãy số (un) bởi công thức truy hồi sau
u
1
0
u
n
+
1
u
n
+...
Đọc tiếp
Cho dãy số (un) bởi công thức truy hồi sau u 1 = 0 u n + 1 = u n + n n ≥ 1 ; u218 nhận giá trị nào sau đây?
A. 23653
B. 46872
C. 23871
D. 23436
Trong các dãy số cho bởi công thức truy hồi sau, hãy chọn dãy số là cấp số nhân A.
u
1
2
u
n
+
1
u...
Đọc tiếp
Trong các dãy số cho bởi công thức truy hồi sau, hãy chọn dãy số là cấp số nhân
A. u 1 = 2 u n + 1 = u n 2
B. u 1 = - 3 u n + 1 = u n + 1
C. u 1 = - 1 u n + 1 = 3 u n
D. u 1 = 3 u n + 1 = 2 n . u n
Đáp án C
Cấp số nhân có công thức truy hồi dạng u 1 = a u n + 1 = q . u n
Dãy số u 1 = - 1 u n + 1 = 3 u n là CSN với u 1 = - 1 và công sai q = 3.
Đúng 0
Bình luận (0)
Cho dãy số (Un) xác định bởi công thức truy hồi:
u
1
-
2
u
n
u
n
-
1...
Đọc tiếp
Cho dãy số (Un) xác định bởi công thức truy hồi: u 1 = - 2 u n = u n - 1 + 2 n , ∀ n ≥ 2 , n ∈ N * . Tìm số hạng tổng quát của dãy số
Trong các dãy số cho bởi công thức truy hồi sau, dãy số nào là cấp số nhân?
A. \({u_1} = - 1,\;{u_{n + 1}} = u_n^2\) B. \({u_1} = - 1,\;{u_{n + 1}} = 2{u_n}\)
C. \({u_1} = - 1,\;{u_{n + 1}} = {u_n} + 2\) D. \({u_1} = - 1,\;{u_{n + 1}} = {u_n} - 2\)
A. Ta có: \(\frac{{{u_n}}}{{{u_{n - 1}}}} = \frac{{u_n^2}}{{{u_n}}} = {u_n}\) phụ thuộc vào n nên (\({u_n})\) thay đổi, do đó\(\left( {{u_n}} \right)\) không phải cấp số nhân.
B. Ta có: \(\frac{{{u_{n + 1}}}}{{{{u_n}}}}= 2\), do đó \(\left( {{u_n}} \right)\) là cấp số nhân với công bội \(q = 2\).
C. Ta có: \({u_{n + 1}}- {u_n} = 2\), do đó \(\left( {{u_n}} \right)\) là cấp số cộng với \(d = 2\) .
D. Ta có: \({u_{n + 1}}- {u_n} = - 2\), do đó \(\left( {{u_n}} \right)\) là cấp số cộng với \(d = -2\).
Vậy ta chọn đáp án B.
Đúng 0
Bình luận (0)
Cho dãy số (Un) xác định bởi công thức truy hồi \(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\dfrac{n+2}{4.\left(n+1\right)}u_n\end{matrix}\right.\), \(n\in\)N*. Công thức số hạng tổng quát của dãy số (Un) là?
Đặt \(\dfrac{u_n}{n+1}=v_n\)
\(GT\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{u_1}{1+1}=1\\v_{n+1}=\dfrac{1}{4}v_n,\forall n\in N\text{*}\end{matrix}\right.\)
\(\Rightarrow v_n=\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)
\(\Rightarrow u_n=\left(n+1\right).\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)
Đúng 3
Bình luận (0)
Dãy số \(\left( {{u_n}} \right)\)cho bởi hệ thức truy hồi: \({u_1} = 1,\;\;\;{u_n} = n.{u_{n - 1}}\) với \(n \ge 2\)
a) Viết năm số hạng đầu của dãy số.
b) Dự đoán công thức số hạng tổng quát \({u_n}\).
a) \({u_1} = 1\)
\( \Rightarrow {u_2} = 2.1 = 2\)
\( \Rightarrow {u_3} = 3.2 = 6\)
\( \Rightarrow {u_4} = 4.6 = 24\)
\( \Rightarrow {u_5} = 5.24 = 120\)
b)
Ta có:
\({u_2} = 2 = 2.1 \)
\({u_3} = 6= 1.2.3 \)
\({u_4} = 24 = 1.2.3.4\)
\({u_5} = 120 = 1.2.3.4.5\)
\( \Rightarrow {u_n} = 1.2.3....n = n!\).
Đúng 0
Bình luận (0)
Cho dãy
u
n
cho bởi công thức truy hồi
u
1
1
2
u
n
+
1...
Đọc tiếp
Cho dãy u n cho bởi công thức truy hồi u 1 = 1 2 u n + 1 = 1 2 − u n nếu n ≥ 1 . Tính giới hạn I của dãy số u n (nếu tồn tại).
A. Không tồn tại giới hạn của dãy u n .
B. I = 2 3 .
C. I = 1 .
D. I = + ∞ .
Đáp án C
Ta có 0 < u 1 < 1 và nếu 0 < u k < 1 thì u k + 1 = 1 2 - u k < 1 nên bằng quy nạp ta có:
0 < u n < 1, ∀ n .
Ta có u 1 = 1 2 < u 2 = 2 3 và nếu u k < u k + 1 thì u k + 2 − u k + 1 = 1 2 − u k + 1 − 1 2 − u k > 0 nên bằng quy nạp ta có: u n < u n + 1 , ∀ n .
Do đó dãy u n tăng và bị chặn nên tồn tại lim u n = I ∈ R .
Ta có
lim u n + 1 = lim 1 2 − u n ⇒ I = 1 2 − I ⇒ − I 2 + 2 I − 1 = 0
⇒ I = 1.
Đúng 0
Bình luận (0)
Cho dãy số
(
u
n
)
xácđịnh bởi công thức truy hồi
u
1
2
u
n
+...
Đọc tiếp
Cho dãy số ( u n ) xácđịnh bởi công thức truy hồi u 1 = 2 u n + 1 = u n + 1 2 v ớ i n ≥ 1
Chứng minh rằng có giới hạn hữu hạn khi Tìm giới hạn đó.
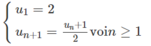
Ta có
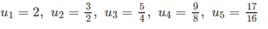
Dự đoán
Chứng minh dự đoán trên bằng quy nạp (bạn đọc tự chứng minh).
Từ đó
Đúng 0
Bình luận (0)
29 tháng 1 2022 lúc 17:44
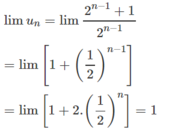
Tìm số hạng tổng quát của dãy số cho bởi công thức truy hồi :
\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=\dfrac{n}{2\left(n+1\right)}.u_n+\dfrac{n+2}{n+1}\end{matrix}\right.\)
\(\left(n+1\right)u_{n+1}=\dfrac{1}{2}nu_n+n+2\)
\(\Leftrightarrow\left(n+1\right)u_{n+1}-2\left(n+1\right)=\dfrac{1}{2}\left[nu_n-2n\right]\)
Đặt \(n.u_n-2n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=-1\\v_{n+1}=\dfrac{1}{2}v_n\end{matrix}\right.\)
\(\Rightarrow v_n=-1.\left(\dfrac{1}{2}\right)^{n-1}\Rightarrow n.u_n-2n=-\dfrac{1}{2^{n-1}}\)
\(\Rightarrow u_n=2-\dfrac{1}{n.2^{n-1}}\)
Đúng 2
Bình luận (0)