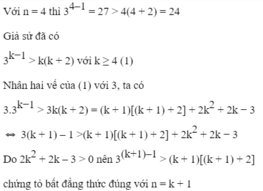Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) sin 2 n α + cos 2 n α ≤ 1 .

Những câu hỏi liên quan
Chứng minh các đẳng thức sau với
n
∈
N
∗
S
n
sin
x
+
sin
2
x
+
.
.
.
+
sin
n
x
sin...
Đọc tiếp
Chứng minh các đẳng thức sau với n ∈ N ∗ S n = sin x + sin 2 x + . . . + sin n x = sin n x 2 . sin n + 1 x 2 sin x 2
iểm tra với n = 1
Giả sử đã có 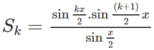
Viết S k + 1 = S k + sin ( k + 1 ) x sử dụng giả thiết quy nạp và biến đổi ta có
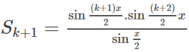
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) 2 n + 2 > 2 n + 5
Với n = 1 thì 2 1 + 2 = 8 > 7 = 2 . 1 + 5
Giả sử bất đẳng thức đúng với n = k ≥ 1 tức là 2k + 2 > 2k + 5 (1)
Ta phải chứng minh nó cũng đúng với n = k + 1,
tức là 2k + 3 > 2(k + 1) + 5 hay 2k + 3 > 2k + 7(2)
Thật vậy, nhân hai vế của (1) với 2, ta được
2k + 3 > 4k + 10 = 2k + 7 + 2k + 3
Vì 2k + 3 > 0 nên 2k + 3 > 2k + 7(đpcm)
Đúng 0
Bình luận (0)
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Chứng minh các bất đẳng thức sau \(\left(n\in N^{\circledast}\right)\):
a) \(2^{n+2}>2n+5\)
b) \(\sin^{2n}\alpha+\cos^{2n}\alpha\le1\)
Cho góc bất kì \(\alpha \). Chứng minh các đẳng thức sau:
a) \({\left( {\sin \alpha + \cos \alpha } \right)^2} = 1 + \sin 2\alpha ;\;\)
b) \({\cos ^4}\alpha - {\sin ^4}\alpha = \cos 2\alpha .\)
a) Ta có: \({\left( {\sin \alpha + \cos \alpha } \right)^2} = {\sin ^2}\alpha + 2\sin \alpha \cos \alpha + {\cos ^2}\alpha = 1 + \sin 2\alpha \;\)
b) \({\cos ^4}\alpha - {\sin ^4}\alpha = \left( {{{\cos }^2}\alpha - {{\sin }^2}\alpha } \right)\left( {{{\cos }^2}\alpha + {{\sin }^2}\alpha } \right) = \cos 2\alpha \;\)
Đúng 0
Bình luận (0)
Chứng minh: \(\frac{3}{2}\ge sin\frac{A}{2}+sin\frac{B}{2}+sin\frac{C}{2}>1\)
P/s: Không dùng bất đẳng thức lượng giác hoặc đẳng thức lượng giác của lớp 10 (nếu dùng thì phải chứng minh lại bằng kiến thức lớp 9)
Chứng minh bất đẳng thức sau: \(\sin\frac{\pi}{15}\sin\frac{\pi}{12}-\cos\frac{\pi}{15}\cos\frac{\pi}{12}:2\sin\frac{7\pi}{12}=\frac{-1}{2}\)
Chứng minh bất đẳng thức sau biết a;b;m;n là các số nguyên: a ^ (m + n) + b ^ (m + n) >= a ^ m * b ^ n + a ^ n * b ^ m
chứng minh bất đẳng thức sau
\(\frac{\sin x+\cos x-1}{1-cosx}=\frac{2cosx}{\sin x-\cos x+1}\)
\(\frac{sinx+cosx-1}{1-cosx}=\frac{\left(sinx+cosx-1\right)\left(sinx-cosx+1\right)}{\left(1-cosx\right)\left(sinx-cosx+1\right)}\)
\(=\frac{sin^2x-\left(cosx-1\right)^2}{\left(1-cosx\right)\left(sinx-cosx+1\right)}=\frac{sin^2x-cos^2x+2cosx-1}{\left(1-cosx\right)\left(sinx-cosx+1\right)}\)
\(=\frac{1-cos^2x-cos^2x+2cosx-1}{\left(1-cosx\right)\left(sinx-cosx+1\right)}=\frac{2cosx-2cos^2x}{\left(1-cosx\right)\left(sinx-cosx+1\right)}\)
\(=\frac{2cosx\left(1-cosx\right)}{\left(1-cosx\right)\left(sinx-cosx+1\right)}=\frac{2cosx}{sinx-cosx+1}\)
Đúng 0
Bình luận (0)