iểm tra với n = 1
Giả sử đã có 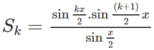
Viết S k + 1 = S k + sin ( k + 1 ) x sử dụng giả thiết quy nạp và biến đổi ta có
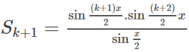
iểm tra với n = 1
Giả sử đã có 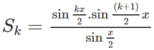
Viết S k + 1 = S k + sin ( k + 1 ) x sử dụng giả thiết quy nạp và biến đổi ta có
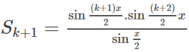
chứng minh đẳng thức lượng giác
a) 2.\(cot\left(\dfrac{\pi}{2}-x\right)\)+ tan\(\left(\pi-x\right)\)= tan\(x\)
b) sin\(\left(\dfrac{5\pi}{2}-x\right)\)+ cos \(\left(13\pi+x\right)\) - sin\(\left(x-5\pi\right)\) = sin\(x\)
chứng minh đẳng thức lượng giác
a) 2.cot\(\left(\dfrac{\pi}{2}-x\right)\)+ tan\(\left(\pi-x\right)\) = tan\(x\)
b) \(sin\left(\dfrac{5\pi}{2}-x\right)\)+ cos\(\left(13\pi+x\right)\) - sin\(\left(x-5\pi\right)\) = sin\(x\)
Giải các PT sau:
1. \(\dfrac{\left(2\cos2x-1\right)\left(\sin x-3\right)}{\sin x}=0\)
2.\(\dfrac{3\left(\sin x+\cos x\right)}{\sin x-\cos x}=2+2\cos x\)
3.\(\dfrac{3\left(\sin x+\tan x\right)}{\tan x-\sin x}-2\cos x=2\)
4. \(1+\sin x+\cos x+\sin2x+\cos2x=0\)
5. \(2\sin x\left(1+\cos2x\right)+\sin2x=1+2\cos x\)
Chứng minh biểu thức sau không phụ thuộc vào x:
Q = \(sinx-sin\left(x+\dfrac{\pi}{5}\right)+sin\left(x+\dfrac{2\pi}{5}\right)-sin\left(x+\dfrac{3\pi}{5}\right)+sin\left(x+\dfrac{4\pi}{5}\right)\)
chứng minh đẳng thức lượng giác
a) \(\dfrac{1-cos^2\left(\dfrac{\pi}{2}-x\right)}{1-sin^2\left(\dfrac{\pi}{2}-x\right)}\) - cot\(\left(\dfrac{\pi}{2}-x\right)\) . tan\(\left(\dfrac{\pi}{2}-x\right)\) = \(\dfrac{1}{sin^2x}\)
b) \(\left(\dfrac{1}{cos2x}+1\right)\).tan\(x\) = \(tan2x\)
giải các phương trình sau :
1. sin( x+\(\pi\)/4)=2/3
2.cos2x-5sinx-3=0
3.cos3x=sin2x
4.cos3x=-\(\sqrt{ }\)3 với -\(\pi\)/2<x<0
5.4sin\(^4\)x + 12cos\(^2\)x=7
6.cot(x-1)=(cos2x)/(1+tanx) + sin\(^2\)x - 1/2sin2x
7.sin\(^2\)3x-cos\(^2\)4x=sin\(^2\)5x-cos\(^2\)6x
chứng minh đẳng thức lượng giác
a) \(\dfrac{1-cos^2\left(\dfrac{\pi}{2}-x\right)}{1-sin^2\left(\dfrac{\pi}{2}-x\right)}\)- cot\(\left(\dfrac{\pi}{2}-x\right)\).tan\(\left(\dfrac{\pi}{2}-x\right)\)= \(\dfrac{1}{sin^2x}\)
b) \(\left(\dfrac{1}{cos2x}+1\right)\).tan\(x\) = tan\(2x\)
Giải các PT sau
1. \(\cos^2\left(x-30^{\cdot}\right)-\sin^2\left(x-30^{\cdot}\right)=\sin\left(x+60^{\cdot}\right)\)
2. \(\sin^22x+\cos^23x=1\)
3. \(\sin x+\sin2x+\sin3x+\sin4x=0\)
4. \(\sin^2x+\sin^22x=\sin^23x\)
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).