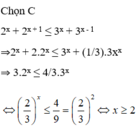\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)

Đáp án A

\(\Leftrightarrow\dfrac{12x+8+7-14x}{4\left(1-2x\right)}-\dfrac{3}{4}\ge0\)

\(\Leftrightarrow\dfrac{-2x+15-3+6x}{4\left(1-2x\right)}\ge0\Leftrightarrow\dfrac{4x+12}{4\left(1-2x\right)}\ge0\)

TH1 : \(\left\{{}\begin{matrix}4x+12\ge0\\1-2x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-3\\x\le\dfrac{1}{2}\end{matrix}\right.\)<=> -3 =< x =< 1/2 

TH2 : \(\left\{{}\begin{matrix}x\le-3\\x\ge\dfrac{1}{2}\end{matrix}\right.\)* vô lí * 

ĐKXĐ: \(x\le2\)

Xét trên miền xác định:

\(\Leftrightarrow\dfrac{2x^3+3x}{7-2x}-1+1-\sqrt{2-x}>0\)

\(\Leftrightarrow\dfrac{\left(x-1\right)\left(2x^2+2x+7\right)}{7-2x}+\dfrac{x-1}{1+\sqrt{2-x}}>0\)

\(\Leftrightarrow\left(x-1\right)\left(\dfrac{2x^2+2x+7}{7-2x}+\dfrac{1}{1+\sqrt{2-x}}\right)>0\)

\(\Leftrightarrow1< x\le2\)

a: Ta có: \(3x+5\le4x-9\)

\(\Leftrightarrow-x\le-14\)

\(\Leftrightarrow x\ge14\)

b: Ta có: \(6-2x< 6-x\)

\(\Leftrightarrow-x< 0\)

hay x>0

c: Ta có: \(7\left(x-1\right)+5>-3x\)

\(\Leftrightarrow7x-7+5+3x>0\)

\(\Leftrightarrow10x>2\)

hay \(x>\dfrac{1}{5}\)

Bài 1: 

a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)

\(\Leftrightarrow6-8x-10+2x-5=0\)

\(\Leftrightarrow-6x+11=0\)

\(\Leftrightarrow-6x=-11\)

hay \(x=\dfrac{11}{6}\)

b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)

\(\Leftrightarrow6-12x-11+3x-1=0\)

\(\Leftrightarrow-9x-6=0\)

\(\Leftrightarrow-9x=6\)

hay \(x=-\dfrac{2}{3}\)

1.

\(6+2x\ge3-x\)

\(\Leftrightarrow3x\ge-3\)

\(\Leftrightarrow x\ge-1\)

2.

\(2x+7>16-x\)

\(\Leftrightarrow3x>23\)

\(\Leftrightarrow x>\dfrac{23}{3}\)

3.

\(x-5< 3x+1\)

\(\Leftrightarrow2x>-6\)

\(\Leftrightarrow x>-3\)

Mik chưa học đến lớp 8 nên ko bt biểu diễn trên trục số nên chỉ tìm dc x thôi nha:

1. 6 + 2x \(\ge\) 3 - x

<=> 6 - 3 \(\ge\) -x - 2x

<=> 3 \(\ge\) -3x

<=> 3 : (-3) \(\ge\) -3x : (-3)

<=> -1 \(\le\) x

<=> x \(\ge\) -1

2. 2x + 7 > 16 - x

<=> 2x + x > 16 - 7

<=> 3x > 9

<=> 3x : 3 > 9 : 3

<=> x > 3

3. x - 5 < 3x + 1

<=> -5 - 1 < 3x - x

<=> -6 < 2x

<=> -6 : 2 < 2x : 2

<=> -3 < x

<=> x > (-3)

1: Ta có: \(2x+6\ge3-x\)

\(\Leftrightarrow3x\ge-3\)

hay \(x\ge-1\)

2: ta có: \(2x+7>16-x\)

\(\Leftrightarrow3x>9\)

hay x>3

3: Ta có: \(x-5< 3x+1\)

\(\Leftrightarrow-2x< 6\)

hay x>-3