Nêu cách giải phương trình trùng phương a x 4 + b x 2 + c = 0 ( a ≠ 0 )

Những câu hỏi liên quan
Nêu cách giải phương trình trùng phương ax4 + bx2 + c = 0 (a ≠ 0)
- Đặt ẩn phụ t = x2 (1) (điều kiện t ≥ 0).
Khi đó phương trình đã cho tương đương với một phương trình bậc 2 ẩn t là:
at2 + bt + c = 0 (2)
- Giải phương trình (2) để tìm t, so sánh với điều kiện.
- Thay giá trị t thỏa mãn vào (1) để tìm x.
Đúng 0
Bình luận (0)
Nêu cách giải phương trình trùng phương
ax4 + bx2 + c = 0 (a ≠ 0)
mình sẽ tick cho ai nhanh nhat
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Bạn tham khảo :
https://toancap2.net/chuyen-de-phuong-trinh-trung-phuong/
Chúc bạn học tốt
1.Nêu cách giải phương trình chứa ẩn ở mẩu?
2. Giải phương trình:
\(\frac{x+2}{x}=\frac{2x+3}{2\left(x-2\right)}\)
1, Các bước giải phương trình chứa ẩn ở mẫu:
Bước 1: Tìm ĐKXĐ của phương trình
Bước 2: Quy đồng và khử mẫu phương trình
Bước 3: Giải phương trình đã khử mẫu
Bước 4: Đối chiếu nghiệm với ĐKXĐ
2, Bạn kiểm tra lại đề
Câu 2 đề đúng mà? Giải PT chứa ẩn ở mẫu đó.
mình test thử xem nào
\(\frac{x+2}{x}=\frac{2x+3}{2\left(x-2\right)}\left(đkxđ:x\ne0;2\right)\)
\(< =>\frac{\left(x+2\right)\left(2x-4\right)}{x\left(2x-4\right)}=\frac{x\left(2x+3\right)}{x\left(2x-4\right)}\)
\(< =>\left(x+2\right)\left(2x-4\right)=x\left(2x+3\right)\)
\(< =>2x^2-4x+4x-8=2x^2+3x\)
\(< =>\left(2x^2-8\right)-\left(2x^2+3x\right)=0\)
\(< =>-8-3x=0\)
\(< =>-8=3x< =>x=\frac{-8}{3}\left(tmđk\right)\)
Vậy nghiệm của pt là \(-\frac{8}{3}\)
Xem thêm câu trả lời
Tìm a để phương trình 2(a - 1)x - a(x - 1) = 2x + 3 . Đáp án: a= 2 (nêu cách giải giúp mình?)
Phương trình nào sau đây ko phải là phương trình bậc 2 ,1 ẩn .nêu cách giải
A)\(\sqrt{2}\) t2 - 2t +4=0 B)(\(\sqrt{9}-3\))x2 + 1 =0
Phương trình A là phương trình bậc hai một ẩn vì a<>0
\(\sqrt{2}t^2-2t+4=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot\sqrt{2}\cdot4=4-16\sqrt{2}< 0\)
Do đó; Phương trình vô nghiệm
Đúng 0
Bình luận (0)
Giải phương trình trên(nêu rõ cách giải):
\(\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-2\sqrt{x-1}}=2\sqrt{2}\)
Giai phương trình theo phương trình trùng phương :
a : x^4 - 13x^2 + 36 =0
b : 5x^4 + 3x^2 - 8 =0
c : 2x^4 + 3x^2 +2 =0
a) \(x^4-13x^2+36=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)\left(x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\\x=-2\\x=-3\end{matrix}\right.\)
b) \(5x^4+3x^2-8=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(5x^2+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)( do \(5x^2+8\ge8>0\))
Đúng 1
Bình luận (0)
c: Ta có: \(2x^4+3x^2+2=0\)
Đặt \(a=x^2\)
Phương trình tương đương là: \(2a^2+3a+2=0\)
\(\text{Δ}=3^2-4\cdot2\cdot2=9-16=-7\)
Vì Δ<0 nên phương trình vô nghiệm
Vậy: Phương trình \(2x^4+3x^2+2=0\) vô nghiệm
Đúng 0
Bình luận (0)
Giải các phương trình trùng phương sau: x 4 + 2 x 2 – x + 1 = 15 x 2 – x – 35
Ta có: x 4 + 2 x 2 – x + 1 = 15 x 2 – x – 35
⇔ x 4 + 2 x 2 – x + 1 - 15 x 2 + x + 35 = 0
⇔ x 4 – 13 x 2 + 36 = 0
Đặt m = x 2 . Điều kiện m ≥ 0
Ta có: x 4 – 13 x 2 + 36 = 0 ⇔ m 2 – 13m + 36 = 0
∆ = - 13 2 – 4.1.36 = 169 – 144 = 25 > 0
∆ = 25 = 5
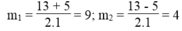
Ta có: x 2 = 9 ⇒ x = ± 3
x 2 = 4 ⇒ x = ± 2
Vậy phương trình đã cho có 4 nghiệm: x 1 = 3; x 2 = -3; x 3 = 2; x 4 = -2
Đúng 0
Bình luận (0)
Giải phương trình 62x – 3 = 1 bằng cách đưa về dạng aA(x) = aB(x) và giải phương trình A(x) = B(x).
\(62x-3=1\\ 62x=4\\ x=\dfrac{4}{62}=\dfrac{2}{31}\)
Đúng 0
Bình luận (0)
6²ˣ⁻³ = 1
⇔ 6²ˣ⁻³ = 6⁰
⇔ 2x - 3 = 0
⇔ 2x = 3
⇔ x = 3/2
Vậy S = {3/2}
Đúng 0
Bình luận (0)



















