Tìm x để mỗi căn thức sau có nghĩa
\(\sqrt{2x+7}\)
Tìm x để mỗi căn thức sau có nghĩa:
2 x + 7
Ta có 2 x + 7 có nghĩa khi 2x+7 ≥ 0
2x + 7 ≥ 0 ⇔ 2x ≥ -7
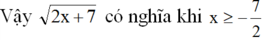
Tìm x để mỗi căn thức sau có nghĩa:
a. \(\sqrt{3-2x}\) b. \(\sqrt{x+1}+\sqrt{3-x}\) c. \(\dfrac{\sqrt{4x-2}}{x^2-4x+3}\) d. \(\dfrac{\sqrt{4x^2-2x+1}}{\sqrt{3-5x}}\)
ĐKXĐ: \(3-2x\ge0\Leftrightarrow x\le\dfrac{3}{2}\)
b) ĐKXĐ: \(-1\le x\le3\)
c) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ne1\\x\ne3\end{matrix}\right.\).
d) ĐKXĐ: \(x< \dfrac{3}{5}\).
Tìm x để các căn thức sau có nghĩa
\(\sqrt{x^2+2x+3}\)
\(x^2+2x+3=\left(x^2+2x+1\right)+2=\left(x+1\right)^2+2\ge2>0\forall x\in R\)
\(\Rightarrow\sqrt{x^2+2x+3}\) xác định với mọi x
Làm như bài trước mik làm, bn chứng minh \(x^2+2x+3\ge0\) là đc
Tìm x để mỗi căn thức sau có nghĩa
\(\sqrt{1+x^2}\)
\(ĐK:x^2+1\ge0\Leftrightarrow x\in R\)
\(1+x^2\ge0\)(luôn đúng)
\(\Rightarrow x\in R\)
Tìm x để mỗi căn thức có nghĩa
a) \(\sqrt{2x+7}\)
b) \(\sqrt{\frac{1}{-1+x}}\)
\(\frac{1}{\sqrt{x-1}}\)
a) sai đề
Tìm x để mỗi căn thức sau có nghĩa\
\(\sqrt{-3x+4}\)
\(-3x+4\ge0\\ \Rightarrow-3x\ge-4\\ \Rightarrow x\le\dfrac{4}{3}\)
Tìm x để mỗi căn thức sau có nghĩa
\(\sqrt{\dfrac{1}{-1+x}}\)
Tìm x để mỗi căn thức sau có nghĩa :
a) \(\sqrt{2x+7}\)
Để \(\sqrt{2x}+7\) có nghĩa thì \(\Leftrightarrow\) 2x + 7 \(\ge\) 0
\(\Leftrightarrow\) 2x \(\ge\) -7
\(\Leftrightarrow\) x \(\ge\) \(\dfrac{-7}{2}\)
vậy khi x \(\ge\) \(\dfrac{-7}{2}\) thì \(\sqrt{2x}+7\) có nghĩa
\(\sqrt{2x}+7\)\(\sqrt{2x}+7\)
Căn thức có nghĩa khi \(2x+7\ge0\Leftrightarrow x\ge-\dfrac{7}{2}\)
Tìm x để căn thức sau có nghĩa a. sqrt(- 3/(1 - 2x)) b.sqrt(2x+5/24)) c.sqrt(2x-16))+x-3/x-8
a: ĐKXĐ: -3/(1-2x)>=0
=>1-2x>0
=>2x<1
=>x<1/2
b: ĐKXĐ: 2x+5/24>=0
=>2x>=-5/24
=>x>=-5/48
c: ĐKXĐ: 2x-16>=0 và x-8<>0
=>x>8
a) Để căn thức sqrt(-3/(1-2x)) có nghĩa, ta cần điều kiện:
1 - 2x > 0 (mẫu số không được bằng 0)
=> 1 > 2x
=> x < 1/2
b) Để căn thức sqrt((2x+5)/24) có nghĩa, ta cần điều kiện:
2x + 5 ≥ 0 (tử số không được âm)
=> 2x ≥ -5
=> x ≥ -5/2
c) Để căn thức sqrt(2x-16) + (x-3)/(x-8) có nghĩa, ta cần thỏa mãn hai điều kiện:
2x - 16 ≥ 0 (căn thức không được âm)
=> 2x ≥ 16
=> x ≥ 8
x ≠ 8 (mẫu số của phân số không được bằng 0)
Vậy, kết hợp hai điều kiện trên, ta có x > 8 và x ≠ 8. Tức là x > 8.