Chọn giá trị f(0) để các hàm số f ( x ) = 2 x + 1 - 1 x ( x + 1 ) liên tục tại điểm x= 0.
A. 1
B. 2
C. 3
D. 4
Chọn giá trị f(0) để các hàm số f ( x ) = 2 x + 1 - 1 x ( x + 1 ) liên tục tại điểm x = 0.
A. 1
B. 2
C. 3
D. 4
Chọn A.
Ta có : 
Vậy để hàm số liên tục tại x = 0 thì f(0) = 1.
Chọn giá trị f(0) để các hàm số f ( x ) = 2 x + 8 3 - 2 3 x + 4 - 2 liên tục tại điểm x = 0
A. 1
B. 2
C. 2/9
D. 1/9
Chọn C.
Ta có :
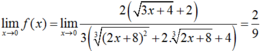
Vậy để hàm số liên tục tại x = 0 ta chọn f(0) = 2/9.
Chọn giá trị f(0) để các hàm số f ( x ) = x + 1 + x - 1 3 x k h i x ≢ 0 2 k h i x = 0 liên tục tại điểm x= 0.
A. Hàm số liên tục tại x 0 = 0
B. Hàm số liên tục tại mọi điểm nhưg gián đoạn tại x 0 = 0
C. Hàm số không liên tục tại x 0 = 0
D. Tất cả đều sai
Cho hàm số y=f(x)=2x^2 -8
a) Tính f(–3) ; f(0) ; f(1) ; f(2) b) Tìm giá trị của x để f(x) có giá trị bằng 0.
a: f(-3)=10
f(0)=-8
f(1)=-6
f(2)=0
b: f(x)=0
=>(x-2)(x+2)=0
=>x=2 hoặc x=-2
1) đạo hàm của hàm số \(\dfrac{2x^2+1}{x^2}\) là
2) cho hàm số \(f\left(x\right)=\sqrt{-5x^2+14x-9}\) tập hợp các giá trị của x để f'(x) = 0 là
1) \(y=\dfrac{2x^2+1}{x^2}\)
\(\Rightarrow y'=\dfrac{\left(4x+1\right)x^2-2x\left(2x^2+1\right)}{x^4}\)
\(\Leftrightarrow y'=\dfrac{4x^3+x^2-4x^3-2x}{x^4}\)
\(\Leftrightarrow y'=\dfrac{x^2-2x}{x^4}=\dfrac{x\left(x-2\right)}{x^4}=\dfrac{x-2}{x^3}\)
2) \(f\left(x\right)=\sqrt[]{-5x^2+14x-9}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-10x+14}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-2\left(5x-7\right)}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}\)
Để \(f'\left(x\right)=0\)
\(f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}=0\)
\(\Leftrightarrow5x-7=0\)
\(\Leftrightarrow5x=7\)
\(\Leftrightarrow x=\dfrac{7}{5}\)
Vậy tập hợp giá trị để \(f'\left(x\right)=0\) là \(\left\{\dfrac{7}{5}\right\}\)
Cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn f(x)>0,∀x∈R. Biết f(0)=1 và (2-x)f(x)-f' (x)=0. Tìm tất cả các giá trị thực của tham số m để phương trình f(x)=m có hai nghiệm phân biệt.
A. m< e 2 .
B. 0<m< e 2 .
C. 0<m≤ e 2 .
D. m > e 2
Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >Cho hàm số \(f\left(x\right)=-x^2-2\left(m-1\right)x+2m-1\). Tìm tất cả các giá trị của tham số \(m\) để \(f\left(x\right)>0,\forall x\in\left(0;1\right)\).
, ( )Cho hàm số ( ) ( )2 2 1 2 1f x x m x m= − − − + − . Tìm tất cả các giá trị của tham số m để ( ) 0f x >, ( )
Ta có \(f\left(x\right)>0,\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-x^2-2\left(m-1\right)x+2m-1>0,\forall x\left(0;1\right)\)
\(\Leftrightarrow-2m\left(x-1\right)>x^2-2x+1,\forall x\in\left(0;1\right)\) (*)
Vì \(x\in\left(0;1\right)\Rightarrow x-1< 0\) nên (*) \(\Leftrightarrow-2m< \dfrac{x^2-2x+1}{x-1}=x-1=g\left(x\right),\forall x\in\left(0;1\right)\)
\(\Leftrightarrow-2m\le g\left(0\right)=-1\Leftrightarrow m\ge\dfrac{1}{2}\)
Cho hàm số y=f(x)=1/2|x|-3
a)Tính f(0); f(-1) ;f(2)
b)Tìm x để f(x)=0
c)Tìm x để f(x)=-2
d)Tìm x để hàm số có giá trị nhỏ nhất
Cho hàm số y=f(x)=1/2|x|-3
a)Tính f(0); f(-1) ;f(2)
b)Tìm x để f(x)=0
c)Tìm x để f(x)=-2
d)Tìm x để hàm số có giá trị nhỏ nhất