Cho E là tập các số tự nhiên có 6 chữ số đôi một khác nhau lập được từ các số 0; 1; 2; 3; 4; 5; 6. Tính xác suất để chọn ngẫu nhiên từ E được một số có dạng a b c d e f ¯ sao cho a + b + c + d = e + f
A . 1 90
B . 4 135
C . 8 225
D . 5 138
Cho tập X={1;2;3...;8}. Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để lập được số chia hết cho 1111 là?
Cho tập hơp X gồm các số TN có 6 chữ số đôi một khác nhau có dạng abcdef. Từ X lấy ngẫu nhiên một số. Tính xs để số lấy ra là số lẻ và t/m a<b<c<d<e<f
Èo toàn bài khó nhằn :( Thôi làm được mỗi câu 2, câu 1 thì...dẹp đi
\(n\left(\Omega\right)=9.9.8.7.6.5\)
Số lẻ vậy thì f={1;3;5;7;9}
Nhưng nếu f=1 thì ko tồn tại a thỏa mãn a<f do a khác 0
f=3 cũng ko thỏa mãn do nếu a=1; b=2; nhưng ko tồn tại c thỏa mãn :v
f=5 tương tự, ko tồn tại e thỏa mãn
=> f={7;9}
Nếu f=7 thì (a,b,c,d,e)={1;2;3;4;5;6} và chỉ có duy nhất 1 cách sắp xếp \(\Rightarrow C^5_6\left(cach\right)\)
Nếu f=9 thì (a,b,c,d,e)={1;2;3;4;5;6;7;8} và chỉ có duy nhất một cách xếp \(\Rightarrow C^5_8\left(cach\right)\)
\(\Rightarrow n\left(A\right)=C^5_6+C^5_8\) \(\Rightarrow p\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)
Gọi A là số tự nhiên có 8 chữ số a1a2a3a4a5a6a7a8 chia hết cho 1111
9999a1a2a3a4 + a1a2a3a4+a5a6a7a8 để A chia hết cho 1111 thì a1a2a3a4+a5a6a7a8 chia hết cho 1111
1000(a1 + a5) + 100(a2 + a6) + 10(a3 + a7) + (a4+ a8) (1) chia hết cho 1111
đặt (a1 + a5) = x
(a2 + a6) = y
(a3 + a7) = z
(a4+ a8) = t
3<=x<=15
xét đk
suy ra x = 9
suy ra x=y=z=t= 9
suy ra x+y+z+t=36 suy ra t= 36-x-y-z
thế vào (1) suy ra
999(a1 + a5) + 99(a2 + a6) + 9(a3 + a7) =36
hoán vị .......
suy ra có 3840 số
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số đôi một khác nhau được lập từ các chữ số 0,1,2,3,4,5,6. Chọn ngẫu nhiên một số từ tập S. Tính xác suất để số được chọn là một số chia hết cho 6
Gọi E là tập hợp các số tự nhiên có 3 chữ số đôi một khác nhau lập được từ các chữ số 1, 2, 3, 4, 7. Chọn ngẫu nhiên một phần tử của E. Tính xác suất để số được chọn chia hết cho 3
A. 1 5
B. 2 5
C. 3 5
D. 4 5
Gọi E là tập hợp các số tự nhiên có 3 chữ số đôi một khác nhau lập được từ các chữ số 1, 2, 3, 4, 7. Chọn ngẫu nhiên một phần tử của E. Tính xác suất để số được chọn chia hết cho 3
A. 1 5
B. 2 5
C. 3 5
D. 4 5
Gọi E là tập hợp các số tự nhiên có 3 chữ số đôi một khác nhau lập được từ các chữ số 1, 2, 3, 4, 7. Chọn ngẫu nhiên một phần tử của E. Tính xác suất để số được chọn chia hết cho 3
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đáp án B.
Số phần tử của E là ![]() .
.
Từ 5 chữ số đã cho ta có 4 bộ gồm 3 chữ số có tổng chia hết cho 3 là ![]() . Mỗi bộ 3 chữ số này ta lập được
. Mỗi bộ 3 chữ số này ta lập được ![]() số thuộc tập hợp E. Vậy trong tập hợp E có
số thuộc tập hợp E. Vậy trong tập hợp E có ![]() số chia hết cho 3.
số chia hết cho 3.
Gọi A là biến cố “Số được chọn từ E chia hết cho 3” thì ![]() .
.
Vậy xác suất cần tính là 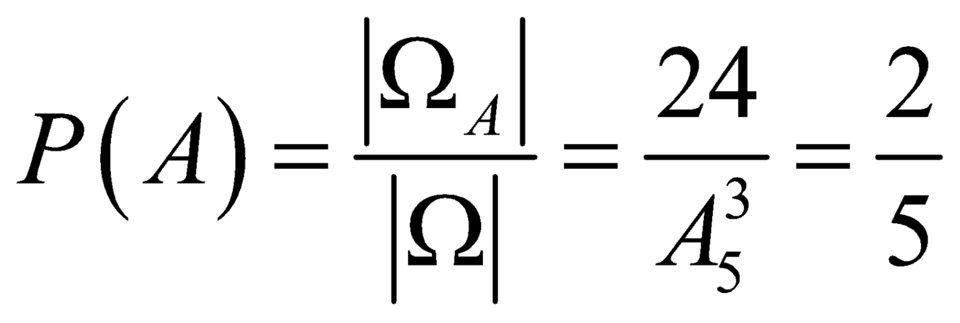 .
.
Câu 1: Từ các số 1; 2; 3; 4; 5; 6; 7. Có thể lập được bao nhiêu số tự nhiên lẻ có 5 chữ số đôi một khác nhau.
Câu 2: Cho tập A gồm các số 0; 1; 2; 3; 4; 5.
a) Có bao nhiêu số tự nhiên có 4 chữ số khác nhau?
b) Chọn ngẫu nhiên 1 số tự nhiên từ các số thành lập ở trên. Tính xác suất để chọn được số chẵn.
1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)
Chọn ngẫu nhiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Gọi S là tích các chữ số của số được chọn. Xác suất đề S > 0 và chia hết cho 6 bằng?
Tham khảo:
https://hoc247.net/cau-hoi-chon-ngau-nhien-mot-so-tu-tap-cac-so-tu-nhien-co-ba-chu-so-doi-mot-khac-nhau-goi-s-la-tich-cac-chu--qid269534.html
gọi s là tập hợp các số tự nhiên có 3 chữ số đôi một khác nhau được lập thành từ các số 0 1 2 3 4 tính xác xuất để trong ba số được lấy ra có đúng một số có chữ số ba
Đề bài chính xác là gì nhỉ? Lấy ra 3 số từ tập đã cho, tính xác suất để trong 3 số có đúng 1 số có chữ số 3?
Số cách lập số có 3 chữ số phân biệt từ tập đã cho: \(4.4.3=48\)
Lấy ra 3 số bất kì: có \(C_{48}^3\) cách
Gọi số có 3 chữ số khác nhau lập từ các số nói trên và luôn có mặt chữ số 3 là abc
TH1: a=3: bc có \(A_4^2=12\) cách chọn
TH2: a khác 3: chọn a có 3 cách, số còn lại có 3 cách, hoán vị nó với 3 cách 2 cách \(\Rightarrow3.3.2=18\) số
\(\Rightarrow12+18=30\) số có mặt chữ số 3 và 18 số không có mặt chữ số 3
Chọn 3 số trong đó có đúng 1 số có mặt chữ số 3: \(C_{30}^1.C_{18}^2\) cách
Xác suất: \(P=\dfrac{C_{30}^1C_{18}^2}{C_{48}^3}=...\)
gọi s là tập hợp tất cả các số tự nhiên có 3 chữ số đôi một khác nhau được lập từ các chữ số 1,2,3,4,5,6. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn là 1 số chia hết cho 5
Không gian mẫu: \(A_6^3=120\)
Gọi số cần lập có dạng \(\overline{abc}\)
Số chia hết cho 5 \(\Rightarrow c=5\) (1 cách chọn)
Chọn và hoán vị cặp ab: \(A_5^2=20\) cách
\(\Rightarrow1.20=20\) số chia hết cho 5
Xác suất: \(P=\dfrac{20}{120}=\dfrac{1}{6}\)