Tọa độ điểm cực đại của đồ thị hàm số là: A. B. C. D.
Đọc tiếp
Tọa độ điểm cực đại của đồ thị hàm số 
là:
A. 
B. 
C. 
D. 
Những câu hỏi liên quan
Cho hàm số
y
f
(
x
)
có bảng biến thiên như hình bên. Tọa độ điểm cực đại của đồ thị hàm số
y
f
(
x
)
là A.
M
(
0
;
-
3
)
B.
N
(
-
1
;
-
4
)
C.
P
(
1
;
-
4
)...
Đọc tiếp
Cho hàm số y = f ( x ) có bảng biến thiên như hình bên. Tọa độ điểm cực đại của đồ thị hàm số y = f ( x ) là
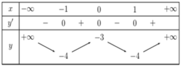
A. M ( 0 ; - 3 )
B. N ( - 1 ; - 4 )
C. P ( 1 ; - 4 )
D. Q ( - 3 ; 0 )
Cho hàm số
y
-
x
3
+
3
x
2
+
m
(m là tham số) có đồ thị (C). Gọi A, B là các điểm cực trị của đồ thị (C). Khi đó, số giá trị của tham số m để diện tích tam giác OAB (O là gốc tọa độ) bằng 1 là: A. 0 B. 2 C. 1 D. 3
Đọc tiếp
Cho hàm số y = - x 3 + 3 x 2 + m (m là tham số) có đồ thị (C). Gọi A, B là các điểm cực trị của đồ thị (C). Khi đó, số giá trị của tham số m để diện tích tam giác OAB (O là gốc tọa độ) bằng 1 là:
A. 0
B. 2
C. 1
D. 3
Bài 6. Cho hàm số y = -2x + 3.
a) Vẽ đồ thị của hàm số trên.
b) Gọi A và B theo thứ tự là giao điểm của đồ thị với các trục Ox và Oy. Tính diện tích tam giác OAB (với O là gốc tọa độ và đơn vị trên các trục tọa độ là centimet ).
c) Tính độ dài đoạn AB
\(b,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow A\left(\dfrac{3}{2};0\right)\Leftrightarrow OA=\dfrac{3}{2}\\ x=0\Leftrightarrow y=3\Leftrightarrow B\left(0;3\right)\Leftrightarrow OB=3\\ \Leftrightarrow S_{OAB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{3}{2}\cdot3=\dfrac{9}{4}\left(cm^2\right)\\ c,C_1:\text{Áp dụng Pytago: }AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\\ C_2:AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}=\sqrt{\left(\dfrac{3}{2}-0\right)^2+\left(0-3\right)^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)
Đúng 2
Bình luận (1)
Cho hàm số
y
x
4
2
-
2
m
2
x
2
+
2
. Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình ph...
Đọc tiếp
Cho hàm số y = x 4 2 - 2 m 2 x 2 + 2 . Tìm tập hợp tất cả các giá trị của tham số thực m sao cho đồ thị của hàm số đã cho có cực đại và cực tiểu, đồng thời đường thẳng cùng phương với trục hoành qua điểm cực đại tạo với đồ thị một hình phẳng có diện tích bằng 64 15 là
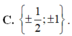
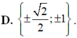
cho hàm số y = 2x+2 có đồ thhij là (d) và hàm số y = -x-1 có đồ thị là (d1)
a, vẽ (d) và (d1) trên cùng 1 mặt phẳng tọa độ trên tọa độ giao điểm của (d) và (d1) bằng phép toán
b, cho hàm số y=(m^2-11) x+m-5 (m là hàm số) co đò thị là (d2).tìm m để đt (d2) cắt đt (d).tìm m dể đt (d2) song song với đường thẳng (d)
Cho hàm số sau d:y= x+2
a) Vẽ đồ thị hàm số trên mặt phẳng tọa độ Oxy
b)Gọi A,B là giao điểm của d với Ox, Oy. Tính diện tích tam giác OAB
c)Tính góc tạo bởi d và trục Ox
a: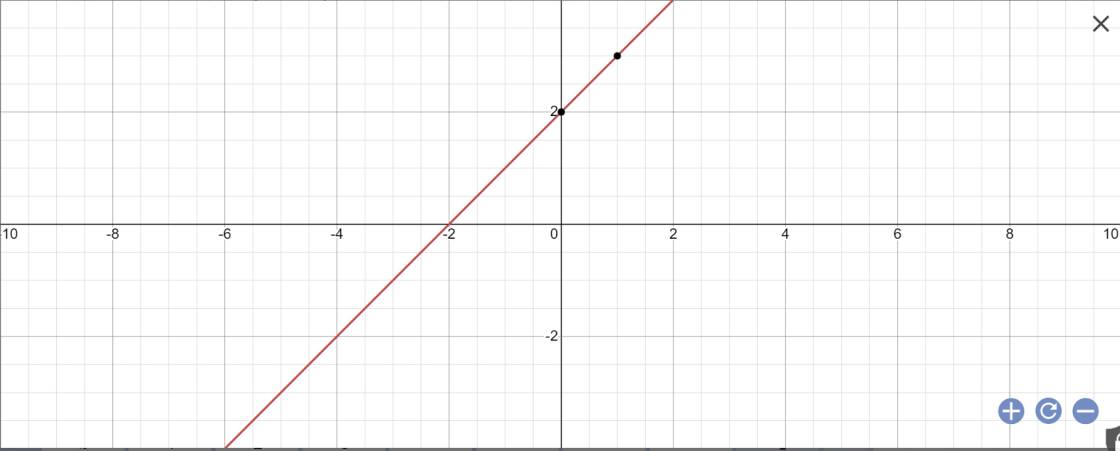 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)
Ox\(\perp\)Oy
mà \(A\in Ox,B\in Oy\)
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
O(0;0); A(-2;0); B(0;2)
\(OA=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{4}=2\)
\(OB=\sqrt{\left(0-0\right)^2+\left(2-0\right)^2}=2\)
ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot AO\cdot OB=\dfrac{1}{2}\cdot2\cdot2=2\)
c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
(d): y=x+2
=>a=1
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
Đúng 1
Bình luận (0)
cho hàm số bậc hất y3x+2 có đồ thị (d) a) vẽ đồ thị (d) b) gọi A và B lần lượt là giao điểm của (d) với trục tung Oy và trục hoành Ox . Tìm tọa độ các điểm A,B. Tính chu vi và diện tích tam giác AOBc)Tính góc tạo bởi đường thangr (d) và trục hoành Ox .(Góc làm tròn đến phút, đơn vị đo trên các trục tọa độ là cm và làm tròng đến chữ số thập phân thứ hai)
Đọc tiếp
cho hàm số bậc hất y=3x+2 có đồ thị (d)
a) vẽ đồ thị (d)
b) gọi A và B lần lượt là giao điểm của (d) với trục tung Oy và trục hoành Ox . Tìm tọa độ các điểm A,B. Tính chu vi và diện tích tam giác AOB
c)Tính góc tạo bởi đường thangr (d) và trục hoành Ox .
(Góc làm tròn đến phút, đơn vị đo trên các trục tọa độ là cm và làm tròng đến chữ số thập phân thứ hai)
a) trong mặt phẳng oxy , vẽ đồ thị hàm số y = -2x
b) Tìm tọa độ điểm B , biết B thuộc đồ thị hàm số trên và B có tung độ là 4
chỉ cần câu b thôi ko cần câu a
Đồ thị của hàm số y x4 – x2 + 1 có bao nhiêu điểm cực trị có tung độ dương? A. 1 B. 2. C. 3. D. 4
Đọc tiếp
Đồ thị của hàm số y = x4 – x2 + 1 có bao nhiêu điểm cực trị có tung độ dương?
A. 1
B. 2.
C. 3.
D. 4
