Trong C, phương trình z - 1 + 3 i = 3 + 2 i có nghiệm là:
A. z = 3 10 - 11 10 i
B. z = - 9 + 7 i
C. z = 3 13 + 11 13 i
D. z = -3 + 6i
Trong không gian Oxyz, cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong của góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng BC có một vectơ chỉ phương là:
A . u → = 2 ; 1 ; - 1
B . u → = 1 ; 1 ; 0
C . u → = 1 ; - 1 ; 0
D . u → = 1 ; 2 ; 1
Chọn C
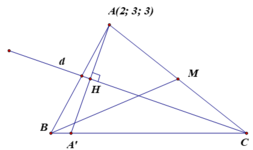
Gọi M là trung điểm của AC. Khi đó M thuộc vào đường trung tuyến kẻ từ B của tam giác ABC.
Giả sử M (3 – t ; 3 + 2t ; 2 – t) ∈ Δ suy ra C (4-2t; 3+4t; 1-2t).
Mà C thuộc và đường phân giác trong d của góc C nên ta có: 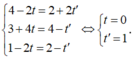
Suy ra C (4; 3; 1).
Gọi H là hình chiếu vuông góc của A trên đường phân giác trong d.
Suy ra H (2+2t';4-t';2-t') ![]()
Ta có ![]() ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
=> H (2;4;2).
Gọi A' đối xứng với A qua đường phân giác trong d.
Suy ra A’ ∈ (BC) và A' (2;5;1). Khi đó ![]() là vectơ chỉ phương của đường thẳng BC.
là vectơ chỉ phương của đường thẳng BC.
Trong không gian Oxyz, cho tam giác ABC có A(2;3;3), phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong của góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng BC có một vectơ chỉ phương là
A. u → = 2 ; 1 ; - 1
B. u → = 1 ; 1 ; 0
C. u → = 1 ; - 1 ; 0
D. u → = 1 ; 2 ; 1
Trong không gian Oxyz, cho tam giác ABC có A ( 2;3;3) phương trình đường trung tuyến kẻ từ B là x − 3 − 1 = y − 3 2 = z − 2 − 1 , phương trình đường phân giác trong của góc C là x − 2 2 = y − 4 − 1 = z − 2 − 1 . Đường thẳng AB có vecto chỉ phương là :
A. u 3 → 2 ; 1 ; − 2
B. u 2 → 1 ; − 1 ; 0
C. u 4 → 0 ; 1 ; − 1
D. u 1 → 1 ; 2 ; 1
Trong không gian O x y z , cho tam giác A B C có A 2 ; 3 ; 3 , phương trình đường trung tuyến kẻ từ B là x − 3 − 1 = y − 3 2 = z − 2 − 1 , phương trình đường phân giác trong của góc C là x − 2 2 = y − 4 − 1 = z − 2 − 1 . Đường thẳng B C có một vectơ chỉ phương là
A. u → = 2 ; 1 ; − 1 .
B. u → = 1 ; 1 ; 0 .
C. u → = 1 ; − 1 ; 0 .
D. u → = 1 ; 2 ; 1 .
Trong không gian Oxyz, cho tam giác ABC có A(2;3;3) phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong của góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng AB có vecto chỉ phương là :
A. (2;1;-2)
B. (1;-1;0)
C. (0;1;-1)
D. (1;2;1)
Đáp án C
Phương pháp:
+) Tam giác ABC có trung tuyến BM và phân giác CD.
+) Tham số hóa tọa độ điểm M là trung điểm của AC, tìm tọa độ điểm C theo tọa độ điểm M.
![]()
+) Tìm tọa độ điểm N đối xứng với M qua CD =>N ∈ BC => Phương trình đường thẳng BC
+) Tìm tọa độ điểm B=BM ∩ BC, khi đó mọi vector cùng phương với AB đều là VTCP của AB.
Cách giải:
Tam giác ABC có trung tuyến BM và phân giác CD.
Gọi M(30t; 3+2t;2-t) ∈ BM là trung điểm của AC ta có
![]()
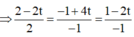
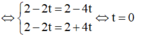
![]()
Gọi H là hình chiếu của M trên CD ta có
![]()
![]()
![]()
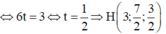
Gọi N là điểm đối xứng với M qua CD => H là trung điểm của MN
![]()
Do CD là phân giác của góc C nên N ∈ BC, do đó phương trình đường thẳng CB là
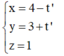
![]()
Xét hệ phương trình
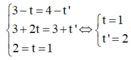
=> B(2;5;1)
![]()
![]()
Bài 1.
a) Kiểm tra xem trong giá trị y = -2, y = 1, giá trị nào là nghiệm của phương trình (y + 1)2 = 2y + 5.
b) Kiểm tra xem trong các giá trị x = -3, x = 1, giá trị nào là nghiệm của phương trình (x + 2)2 = 4x + 5.
c) Kiểm tra xem trong các giá trị t = -1, t = 3, giá trị nào là nghiệm của phương trình (2t + 1)2 = 4t + 5.
d) Kiểm tra xem trong các giá trị z = -2, z = 1, giá trị nào là nghiệm của phương trình (z + 3)2 = 6z + 10.
a, +) Thay y = -2 vào phương trình trên ta có :
( -2 + 1 )2 = 2 . ( -2 ) + 5
1 = 1
Vậy y = -2 thỏa mãn phương trình trên
+) Thay y = 1 vào phương trình trên , ta có :
( 1 + 1)2 = 2 . 1 + 5
4 = 7
Vậy y = 1 thỏa mãn phương trình trên
b, +) Thay x =-3 vaò phương trình trên , ta có :
( -3 + 2 )2 = 4 . ( -3 ) + 5
2 = -7
Vậy x = -3 không thỏa mãn phuong trình trên
+) Thay x = 1 vào phương trình trên , ta có :
( 1 + 2 )2 = 4 . 1 + 5
9 = 9
Vậy x = 1 thỏa mãn phương trình trên
c, +) Thay t = -1 vào phương trình , ta có :
[ 2 . ( -1 ) + 1 ]2 = 4 . ( -1 ) + 5
1 = 1
Vậy t = -1 thỏa mãn phương trình trên
+) Thay t = 3 vào phương trình trên , ta có :
( 2 . 3 + 1 )2 = 4 . 3 + 5
49 = 17
Vậy t = 3 không thỏa mãn phương trình trên
d, +) Thay z = -2 vào phương trình trên , ta có :
( -2 + 3 )2 = 6 . ( -2 ) + 10
1 = -2
Vậy z = -2 không thỏa mãn phương trình trên
+) Thay z = 1 vào phương trình trên , ta có :
( 1 + 3 )2 = 6 . 1 + 10
16 = 16
Vậy z =1 thỏa mãn phương trình trên
Phương trình nào dưới đây nhận z=1+ 3 i và z=1-√3 i làm nghiệm?
A. z 2 - 2 z + 3 = 0 .
B. z 2 - 2 z + 4 = 0 .
C. z 2 + 2 z + 3 = 0 .
D. z 2 + 2 z + 4 = 0 .
Tìm nghiệm của phương trình: ( z + 3 - i)2 - 6( z + 3 - i) + 13 = 0
A. z = 3i; z = 1 - 2i
B. z = - i; z = 3i + 4
C. z = 3i + 4; z = 3i
D. z = 3i; z = -i
Chọn D.
Đặt t = z + 3 - i. Phương trình đã cho trở thành: t2 - 6t + 13 = 0
Suy ra : t = 3 + 2i hoặc t = 3 - 2i
Với t = 3+ 2i thì z + 3 – I = 3 + 2i hay z = 3i
Với t = 3- 2i thì z + 3 – I = 3 -2i hay z = - i
Số nghiệm phức của phương trình z + 2 | z | + 3 - i = ( 4 + i ) | z | z là
A. 1.
B. 2.
C. 3.
D. 4.