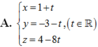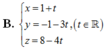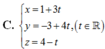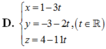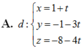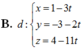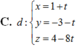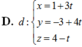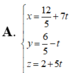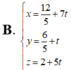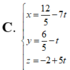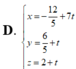Question

Trong không gian Oxyz, cho tam giác ABC có A(2;3;3) phương trình đường trung tuyến kẻ từ B là  x - 3 - 1 = y - 3 2 = z - 2 - 1 ,  phương trình đường phân giác trong của góc C là  x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng AB có vecto chỉ phương là :

A. (2;1;-2)

B. (1;-1;0)

C. (0;1;-1) 

D. (1;2;1)

Answer 1

Đáp án C

Phương pháp:

+) Tam giác ABC có trung tuyến BM và phân giác CD.

+) Tham số hóa tọa độ điểm M là trung điểm của AC, tìm tọa độ điểm C theo tọa độ điểm M.

+) Tìm tọa độ điểm N đối xứng với M qua CD =>N ∈ BC => Phương trình đường thẳng BC

+) Tìm tọa độ điểm B=BM ∩ BC, khi đó mọi vector cùng phương với AB đều là VTCP của AB.

Cách giải:

Tam giác ABC có trung tuyến BM và phân giác CD.

Gọi M(30t; 3+2t;2-t) ∈ BM là trung điểm của AC ta có 

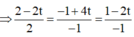
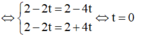
Gọi H là hình chiếu của M trên CD ta có 

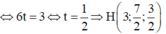
Gọi N là điểm đối xứng với M qua CD => H là trung điểm của MN 

Do CD là phân giác của góc C nên N ∈ BC, do đó phương trình đường thẳng CB là

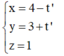
Xét hệ phương trình 

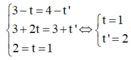
=> B(2;5;1)