Cho hình phẳng A giới hạn bởi đồ thị hai hàm số y=x2 và y=6-|x|.Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là
A. 32π3
B. 8π
C. 9π
D. 20π
Những câu hỏi liên quan
Cho hình phẳng A giới hạn bởi đồ thị hai hàm số
y
x
2
và
y
6
−
x
.
Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là A.
32
π
3
B.
8
π
C.
20
π
D.
6
π
Đọc tiếp
Cho hình phẳng A giới hạn bởi đồ thị hai hàm số y = x 2 và y = 6 − x . Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là
A. 32 π 3
B. 8 π
C. 20 π
D. 6 π
Cho hình phẳng A giới hạn bởi đồ thị hai hàm số
y
x
2
v
à
y
6
-
x
.Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là:
Đọc tiếp
Cho hình phẳng A giới hạn bởi đồ thị hai hàm số y = x 2 v à y = 6 - x .Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là:
Cho hình phẳng H giới hạn bởi đồ thị hàm số
y
x
2
v
à
y
2
−
x
. Tính thể tích V của khối tròn xoay tạo được khi quay H xung quanh trục tung. A.
V
13
π
3
B.
V
5
π
6...
Đọc tiếp
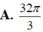
Cho hình phẳng H giới hạn bởi đồ thị hàm số y = x 2 v à y = 2 − x . Tính thể tích V của khối tròn xoay tạo được khi quay H xung quanh trục tung.
A. V = 13 π 3
B. V = 5 π 6
C. 16 π
D. 8 π
Cho hình phẳng H giới hạn bởi đồ thị hàm số
y
x
2
và
y
2
-
x
. Tính thể tích V của khối tròn xoay tạo được khi quay H xung quanh trục tung.
Đọc tiếp
Cho hình phẳng H giới hạn bởi đồ thị hàm số y = x 2 và y = 2 - x . Tính thể tích V của khối tròn xoay tạo được khi quay H xung quanh trục tung.
Cho hàm số
y
f
x
trên đoạn
a
;
b
. Gọi D là diện tích hình phẳng giới hạn bởi đồ thị hàm số
y
f
x
, trục hoành và hai đường thẳng
x
a
,
x
b
a
b
....
Đọc tiếp
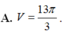
Cho hàm số y = f x trên đoạn a ; b . Gọi D là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x , trục hoành và hai đường thẳng x = a , x = b a < b . Thể tích khối tròn xoay tạo thành khi quay D xung quanh trục hoành được tính theo công thức:
A. V = π ∫ a b f 2 x d x
B. V = π 2 ∫ a b f x d x
C. V = π 2 ∫ a b f 2 x d x
D. V = 2 π ∫ a b f 2 x d x
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
(
x
-
2
)
.
e
2
x
, trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng
π
(
e
a
+
b...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = ( x - 2 ) . e 2 x , trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng π ( e a + b ) c . Khi đó a+b+c bằng
A. 2
B. 56
C. -1
D. -24
Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là:
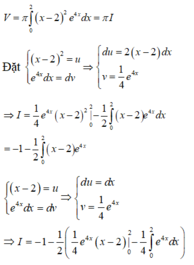
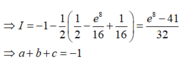
Đáp án C
Đúng 0
Bình luận (0)
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
x
-
2
e
2
x
, trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng
π
e
2...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x - 2 e 2 x , trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng π e 2 + b c ; a ; b ; c ∈ Z . Khi đó a + b + c bằng
A. 2
B. 56
C. -1
D. -24
Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là:
V = π ∫ 0 2 x - 2 2 e 4 x dx = π . l
Đặt
x - 2 2 = u e 4 x d x = d v ⇒ d u = 2 x - 2 d x v = 1 4 e 4 x
⇒ t = 1 4 e 4 x x - 2 2 0 2 - 1 2 ∫ 0 2 x - 2 e 4 x d x = - 1 - 1 2 ∫ 0 2 x - 2 e 4 x
Đặt
x - 2 2 = u e 4 x d x = d v ⇒ d u = d x v = 1 4 e 4 x ⇒ I = - 1 - 1 2 1 4 e 4 x x - 2 0 2 - 1 4 ∫ 0 2 e 4 x d x ⇒ I = - 1 - 1 2 1 2 - e 8 16 + 1 16 = e 8 - 41 32 ⇒ a + b + c = - 1
Đáp án cần chọn là C
Đúng 0
Bình luận (0)
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
x
-
2
e
2
x
,
trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng
π
e
a
+...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x - 2 e 2 x , trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng π e a + b c ; a , b , c ∈ Z . Khi đó a + b + c bằng
A. 2
B. 56
C. -1
D. -24
Cho hàm số
y
f
x
liên tục trên đoạn
a
;
b
.
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y
f
x
, trục hoành và hai đường thẳng
x
a...
Đọc tiếp
Cho hàm số y = f x liên tục trên đoạn a ; b . Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f x , trục hoành và hai đường thẳng x = a , x = b a < b . Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
A. V = π ∫ a b f 2 x d x .
B. V = 2 π ∫ a b f 2 x d x .
C. V = π 2 ∫ a b f 2 x d x .
D. V = π 2 ∫ a b f x d x .