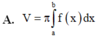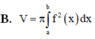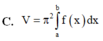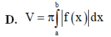Các câu hỏi tương tự
Cho hình phẳng A giới hạn bởi đồ thị hai hàm số
y
x
2
v
à
y
6
-
x
.Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là:
Đọc tiếp
Cho hình phẳng A giới hạn bởi đồ thị hai hàm số y = x 2 v à y = 6 - x .Thể tích khối tròn xoay tạo được khi quay A xung quanh trục tung là:
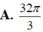
![]()
![]()
![]()
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
(
x
-
2
)
.
e
2
x
, trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng
π
(
e
a
+
b...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = ( x - 2 ) . e 2 x , trục tung và trục hoành. Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox có dạng π ( e a + b ) c . Khi đó a+b+c bằng
A. 2
B. 56
C. -1
D. -24
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
(
x
-
1
)
e
2
x
, trục tung và đường thẳng y 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox A.
V
π
2
e
4
-
13
B. ...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = ( x - 1 ) e 2 x , trục tung và đường thẳng y = 0. Tính thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục Ox
A. V = π 2 e 4 - 13
B. V = π 32 e 4 + 4
C. V = π 32 e 4 - 11
D. V = π 32 e 4 - 5
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
1
cos
x
; y 0; x 0;
x
π
3
Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là.
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 1 cos x ; y = 0; x = 0; x = π 3 Thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox là.
![]()
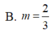
![]()
![]()
Cho số thực dương a, kí hiệu H là hình phẳng giới hạn bởi đồ thị hàm số
y
4
(
x
-
a
)
e
x
, trục hoành và trục tung. Gọi V là thể tích của khối tròn xoay tạo thành khi quay H quanh trục hoành, tìm a biết
V
4
π
(
e
2
-
5
)
.
Đọc tiếp
Cho số thực dương a, kí hiệu H là hình phẳng giới hạn bởi đồ thị hàm số y = 4 ( x - a ) e x , trục hoành và trục tung. Gọi V là thể tích của khối tròn xoay tạo thành khi quay H quanh trục hoành, tìm a biết V = 4 π ( e 2 - 5 ) .
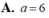
![]()
![]()
![]()
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số
y
x
e
x
và các đường thẳng x1; x2; y0. Tính thể tích V của khối tròn xoay thu được khi quay hình D xung quanh trục Ox.
Đọc tiếp
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = x e x và các đường thẳng x=1; x=2; y=0. Tính thể tích V của khối tròn xoay thu được khi quay hình D xung quanh trục Ox.
![]()
![]()
![]()
![]()
Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
x
(
x
−
1
)
2
và trục hoành. Khi quay (H) quanh trục Ox ta được một khối tròn xoay có thể tích là A.
1
12
B.
π
12
C.
1
105
D.
π...
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x ( x − 1 ) 2 và trục hoành. Khi quay (H) quanh trục Ox ta được một khối tròn xoay có thể tích là
A. 1 12
B. π 12
C. 1 105
D. π 105
Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
x
(
x
-
1
)
2
và trục hoành. Khi quay (H) quanh trục Ox ta được một khối tròn xoay có thể tích là: A.
1
12
. B.
π
12
. C.
1
105
....
Đọc tiếp
Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số y = x ( x - 1 ) 2 và trục hoành. Khi quay (H) quanh trục Ox ta được một khối tròn xoay có thể tích là:
A. 1 12 .
B. π 12 .
C. 1 105 .
D. π 105 .
Cho hàm số y f(x) liên tục trên đoạn [a;b]. Thể tích V của khối nón tròn xoay thu được khi cho hình phẳng (H) giới hạn bởi đồ thị của y f(x); x a; x b khi quay xung quanh trục Ox tính bằng công thức:
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b]. Thể tích V của khối nón tròn xoay thu được khi cho hình phẳng (H) giới hạn bởi đồ thị của y = f(x); x = a; x = b khi quay xung quanh trục Ox tính bằng công thức: