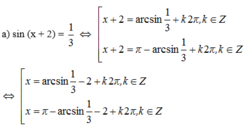\(2sinx-1=0\)

\(\Leftrightarrow sinx=\dfrac{1}{2}\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

a) \(\sin x = \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \sin x = \sin \frac{\pi }{4}\;\;\;\; \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi  - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;\)

b)

\(\begin{array}{l}\sin 3x =  - \sin 5x\;\;\;\\\; \Leftrightarrow \,\,\,\sin 3x + \sin 5x = 0\;\;\;\;\;\;\\ \Leftrightarrow \,\,\,2\sin 4x\cos x = 0\;\end{array}\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = 0}\\{\cos x = 0}\end{array}\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = \sin 0}\\{\cos x = \cos \frac{\pi }{2}}\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x = k\pi }\\{x = \frac{\pi }{2} + k\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.} \right.\)

-√2/2 = sin⁡(-45o) nên sin⁡(x + 45o ) = (-√2)/2

⇔ sin⁡(x+45o) = sin⁡(-45o)

Khi đó,x + 45o = -45o + k360o, k ∈ Z

⇒ x = -45o - 45o + k360o, k ∈ Z

và x + 45o = 180o - (-45o ) + k360o, k ∈ Z

⇒ x = 180o - (-45o ) - 45o + k360o,k ∈ Z

Vậy: x = -90o + k360o, k ∈ Z và x = 180o + k360o, k ∈ Z

ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)

\(\dfrac{cosx}{sinx}-1=\dfrac{cos^2x-sin^2x}{1+\dfrac{sinx}{cosx}}+sin^2x-sinx.cosx\)

\(\Leftrightarrow\dfrac{cosx-sinx}{sinx}=cosx\left(cosx-sinx\right)-sinx\left(cosx-sinx\right)\)

\(\Leftrightarrow\left(cosx-sinx\right)\left(\dfrac{1}{sinx}-cosx+sinx\right)=0\)

\(\Leftrightarrow\left(cosx-sinx\right)\left(1-sinx.cosx+sin^2x\right)=0\)

\(\Leftrightarrow\left(cosx-sinx\right)\left(3-sin2x-cos2x\right)=0\)

\(\Leftrightarrow\left(cosx-sinx\right)\left(3-\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\right)=0\)

1.

PT $\Leftrightarrow 2^{x^2-5x+6}+2^{1-x^2}-2^{7-5x}-1=0$

$\Leftrightarrow (2^{x^2-5x+6}-2^{7-5x})-(1-2^{1-x^2})=0$

$\Leftrightarrow 2^{7-5x}(2^{x^2-1}-1)-(2^{x^2-1}-1)2^{1-x^2}=0$

$\Leftrightarrow (2^{x^2-1}-1)(2^{7-5x}-2^{1-x^2})=0$

$\Rightarrow 2^{x^2-1}-1=0$ hoặc $2^{7-5x}-2^{1-x^2}=0$

Nếu $2^{x^2-1}=1\Leftrightarrow x^2-1=0$

$\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1$

$2^{7-5x}-2^{1-x^2}=0$

$\Leftrightarrow 7-5x=1-x^2\Leftrightarrow x^2-5x+6=0$

$\Leftrightarrow (x-2)(x-3)=0\Leftrightarrow x=2; x=3$

2. Đặt $\sin ^2x=a$ thì $\cos ^2x=1-a$. PT trở thành:

$16^a+16^{1-a}=10$

$\Leftrightarrow 16^a+\frac{16}{16^a}=10$

$\Leftrightarrow (16^a)^2-10.16^a+16=0$

Đặt $16^a=x$ thì:

$x^2-10x+16=0$

$\Leftrightarrow (x-2)(x-8)=0$

$\Leftrightarrow x=2$ hoặc $x=8$

$\Leftrightarrow 16^a=2$ hoặc $16^a=8$

$\Leftrightarrow 2^{4a}=2$ hoặc $2^{4a}=2^3$

$\Leftrightarroww 4a=1$ hoặc $4a=3$

$\Leftrightarrow a=\frac{1}{4}$ hoặc $a=\frac{3}{4}$

Nếu $a=\frac{1}{4}\Leftrightarrow \sin ^2x=\frac{1}{4}$

$\Leftrightarrow \sin x=\pm \frac{1}{2}$

Nếu $a=\sin ^2x=\frac{3}{4}\Rightarrow \sin x=\pm \frac{\sqrt{3}}{2}$

Đến đây thì đơn giản rồi.

hị ơi chị giải hộ em bài bên dưới với

giúp e

toi la con trai