Tìm tọa độ của chân đường vuông góc chung của B'D' và BC'.

Những câu hỏi liên quan
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' với \(A\left(0;0;0\right),B\left(1;0;0\right),D\left(0;1;0\right),A'\left(0;0;1\right)\)
a) Hãy tìm tọa độ các đỉnh còn lại
b) Chứng minh \(A'C\perp\left(BC'D\right)\)
c) Tìm tọa độ của chân đường vuông góc chung của B'D và BC'
trong hệ trục tọa độ oxy, cho đường tròn tâm O. Gọi H(-1;0) và K(1;1) lần lượt là chân các đường vuông góc kẻ từ B và C của tam giác ABC. Tìm tọa độ các đỉnh của tam giác ABC, biết A thuộc d:3x-y-1=0
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, BC = c.
a) Tính khoảng cách giữa CC' và (BB'D'D).
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.

a) Trong (ABCD) kẻ \(CE \bot BD\)
Mà \(CE \bot BB'\left( {BB' \bot \left( {ABCD} \right)} \right) \Rightarrow CE \bot \left( {BB'D'D} \right)\)
Ta có CC’ // BB’ \( \Rightarrow \) CC’ // (BB’D’D) \( \Rightarrow \) d(CC’, (BB’D’D)) = d(C, (BB’D’D)) = CE
Xét tam giác BCD vuông tại C có
\(\frac{1}{{C{E^2}}} = \frac{1}{{B{C^2}}} + \frac{1}{{C{D^2}}} = \frac{1}{{{c^2}}} + \frac{1}{{{b^2}}} = \frac{{{b^2} + {c^2}}}{{{c^2}{b^2}}} \Rightarrow CE = \frac{{bc}}{{\sqrt {{b^2} + {c^2}} }}\)
b) \(AC \subset \left( {ABCD} \right),B'D' \subset \left( {A'B'C'D'} \right),\left( {ABCD} \right)//\left( {A'B'C'D'} \right)\)
\( \Rightarrow d\left( {AC,B'D'} \right) = d\left( {\left( {ABCD} \right),\left( {A'B'C'D'} \right)} \right) = BB' = a\)
Đúng 0
Bình luận (0)
trong hệ trục tọa độ oxy, cho đường tròn tâm O. Gọi H(-1;0) và K(1;1) lần lượt là chân các đường vuông góc kẻ từ B và C của tam giác ABC. Tìm tọa độ các đỉnh của tam giác ABC, biết A thuộc d:3x-y-1=0
Trong mặt phẳng hệ tọa độ Oxy, cho hình vuông ABCD và điểm E thuộc cạnh BC. Một đường thẳng qua A vuông góc với AE cắt CD tại F. Đường thẳng chứa đường trung tuyến AM của tam giác AEF cắt CD tại K. Tìm tọa độ điểm D biết A(-6;6). M(-4;2) và K(-3;0)
Có 2 tam giác vuông \(\Delta ABE=\Delta ADF\) vì \(AB=AD\) và \(\widehat{BAE}=\widehat{DAF}\) cùng phụ với \(\widehat{DAE}\)
Suy ra tam giác AEF vuông cân và \(ME=MA=MF\Rightarrow AM\perp EF\)
Ta có \(\overrightarrow{MA}=\left(2;-4\right)\), đường thẳng EF đi qua M có phương trình :
\(2\left(x+4\right)-4\left(y-2\right)=0\Leftrightarrow x-2y+8=0\)
Bây giờ tìm tọa độ các điểm E, F thỏa mãn ME=MA=MF. Gọi T(x;y) thuộc đường thẳng EF, thì x=2t-8; y=t, \(t\in R\)
Khi đó \(MT=MA\Leftrightarrow\left(2t-8+4\right)^2+\left(1-2\right)^2=2^2+\left(-4\right)^2=20\)
\(\Leftrightarrow5\left(t-2\right)^2=20\Leftrightarrow t\left(t-4\right)=0\Leftrightarrow\)\(\begin{cases}t=0\\t=4\end{cases}\)
Như vậy có 2 điểm \(t_1\left(-8;0\right);t_2\left(0;4\right)\) ( Chính là 2 điểm E và F) thuộc đường thẳng EF mà \(MT_1=MA\)
- Trường hợp \(E\left(-8;0\right);F\left(0;4\right)\). Do F thuộc đường thẳng CD nên đường thẳng CD nhận \(\overrightarrow{KF}=\left(3;4\right)\) làm vec tơ chỉ phương.
Phương trình đường thẳng CD là \(\begin{cases}x=3t\\y=4+4t\end{cases}\) (\(t\in R\)).
Khi đó \(D\left(3t;4+4t\right)\)
Ta có \(AD\perp KF\Leftrightarrow\overrightarrow{KF}.\overrightarrow{AD}=0\Rightarrow3\left(3t+6\right)+4\left(-2+4t\right)=0\Leftrightarrow t=-\frac{2}{5}\Rightarrow D\left(-\frac{6}{5};\frac{12}{5}\right)\)
- Trường hợp \(F\left(-8;0\right);E\left(0;4\right)\), đường thẳng CD nhận \(\overrightarrow{FK}=\left(5;0\right)\) làm vec tơ chỉ phương
Phương trình CD : \(\begin{cases}x=-8+5t\\y=0\end{cases}\) \(\left(t\in R\right)\)
Khi đó \(D\left(-8+5t;0\right)\)
Ta có \(AD\perp KF\Leftrightarrow\overrightarrow{FK}.\overrightarrow{AD}=0\Leftrightarrow5\left(-2+5t\right)=0\Leftrightarrow t=\frac{2}{5}\Rightarrow D\left(-6;0\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy Cho tam giác ABC nội tiếp trong đường tròn tâm I; có đỉnh A thuộc đường thẳng d: x + y - 2 = 0, D(2; -1) là chân đường cao của tam giác ABC hạ từ đỉnh A. Gọi điểm E(3; 1) là chân đường vuông góc hạ từ B xuống AI; điểm P(2;1) thuộc đường thẳng AC. Tìm tọa độ các đỉnh của tam giác ABC.
MAT DAY LOP 6,7,8,9 MA DUA LOP 1 , MAT DAY DI MA
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1; 3) và B (4; 2). Tìm tọa độ điểm E là chân đường phân giác trong góc O của tam giác OAB A.
E
5
2
;
5
2
.
B.
E
3
2
;
−...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1; 3) và B (4; 2). Tìm tọa độ điểm E là chân đường phân giác trong góc O của tam giác OAB
A. E = 5 2 ; 5 2 .
B. E = 3 2 ; − 1 2 .
C. E = − 2 + 3 2 ; 4 + 2 .
D. E = − 2 + 3 2 ; 4 − 2 .
Theo tính chất đường phân giác của tam giác ta có E A E B = O A O B = 2 2 .
Vì E nằm giữa hai điểm A, B nên E A → = − 2 2 E B → . *
Gọi E(x; y). Ta có E A → = 1 − x ; 3 − y E B → = 4 − x ; 2 − y .
Từ (*), suy ra 1 − x = − 2 2 4 − x 3 − y = − 2 2 2 − y ⇔ x = − 2 + 3 2 y = 4 − 2 .
Chọn D.
Đúng 0
Bình luận (0)
Trong hệ tọa độ Oxyz, lập phương trình đường vuông góc chung
△
của hai đường thẳng
d
1
:
x
-
1
1
y
-
3
-
1
z
-
2
2
và
d
2
:
...
Đọc tiếp
Trong hệ tọa độ Oxyz, lập phương trình đường vuông góc chung △ của hai đường thẳng d 1 : x - 1 1 = y - 3 - 1 = z - 2 2 và d 2 : x = - 3 t y = t z = - 1 - 3 t
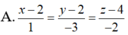
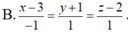
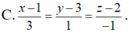
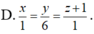
Trong mp tọa độ Oxy, cho A(3;0), B(2;4). Gọi D là chân đường phân giác trong góc O của tam giác ABC. Tìm tọa độ của D.





















