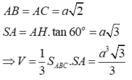cho tam giác ABC đều có đường cao AH = 3 căn 3. Tính SABC

Những câu hỏi liên quan
1. Cho tam giác ABC cân tại A, đg cao AH, O là tđ của AH, BO và CO cắt AB,AC tại D,E. Tính Sadoe biết Sabc=108cm2
2,Cho tam giác ABC cân tại A, có 2 đg cao AH=10,BD=12. Tính Sabc
3, cho tam giác ABC có AB=20, AC=34,BC=42. Tính Sabc
Bạn nào làm gấp giúp mk vs ạ, thanks trước
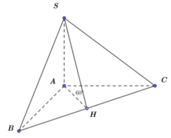
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng
60
0
.Tính theo a thể tích khối tứ diện SABC
A
.
a
3
6
3
B
.
a...
Đọc tiếp
Cho tứ diện SABC có ABC là tam giác vuông cân tại A, đường cao SA. Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60 0 .Tính theo a thể tích khối tứ diện SABC
A . a 3 6 3
B . a 3 3 3
C . 2 a 3 6 3
D . a 3 2 3
cho tam giác vuông ABC. Biết tỉ lệ AB/AC =3/4 và AH là đường cao =24 cm. tính Sabc
AB/AC=3/4
=>HB/HC=9/16
=>HB=9/16HC
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{9}{16}=24^2\)
\(\Leftrightarrow HC=32\left(cm\right)\)
=>HB=18(cm)
=>BC=50(cm)
\(S_{ABC}=\dfrac{BC\cdot AH}{2}=\dfrac{50\cdot24}{2}=25\cdot24=600\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho hình chóp SABC có đáy ABC là tam giác đều , tam giác SBC có đường cao SH =h và (SBC ) _|_ (SBC) . Cho biết SB hợp với (ABC) một góc 30° .Tính thể tích hình chóp SABC
Gọi H là chiều dài vuông góc của S trên BC.
(SBC)_I_(ABC)
(SBC) \(\cap\) (ABC) = BC
SH \(\subset\) (SBC)
SH _I_ BC
SH là đường cao hình chóp S.ABC
.Ta có : SH = SB sinSBC = \(a\sqrt{3}\)
S.ABC = 1/2 BA . BC
V.S.ABC = 1/3 SH . S.ABC 2a3\(\sqrt{3}\)
Đúng 0
Bình luận (0)
Cho tam giác abc có 3 góc nhọn, đường cao ah. CM:
a) Sin A +Cos B >1. b) cho bc=12, góc b=60, góc c=45. Tính Sabc
Cho tam giác ABC đều , nội tiếp đường tròn O , bán kính bằng căn bậc hai của 3, đường cao AH
a. CM: AO=2OH
b. Tìm cạnh tam giác đều ABC
Cho tam giác ABC, vuông tại A đường cao AH. Biết AH = 2 căn 3, góc BAH = 60 độ. Tính bán kính đường tròn đi qua ba đỉnh của tam giác ABC
Xét \(\Delta\) vuông tại H \(ABH\) có :
\(tan\widehat{BAH}=tan60^o=\dfrac{BH}{AH}\Rightarrow BH=AH.tan60^o=2\sqrt[]{3}.\sqrt[]{3}=6\)
Xét \(\Delta\) vuông tại H \(ACH\) có :
\(\widehat{HAC}=90^o-\widehat{BAH}=90^o-60^o=30^o\)
\(tan\widehat{HAC}=tan30^o=\dfrac{CH}{AH}\Rightarrow CH=AH.tan30^o=2\sqrt[]{3}.\dfrac{1}{\sqrt[]{3}}=2\)
Tâm đường tròn ngoại tiếp tam giác vuông ABC là trung điểm BC
\(\Rightarrow\) Bán kính đường tròn này là :
\(R=\dfrac{BC}{2}=\dfrac{BH+CH}{2}=\dfrac{6+2}{2}=4\)
Đúng 1
Bình luận (0)
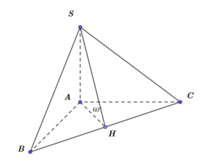
Cho tứ diện SABCD có ABC là tam giác vuông cân tại A, đường cao SA Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng
60
°
.Tính theo a thể tích khối tứ diện SABC A.
a
3
6
3
B.
a
3
3
3...
Đọc tiếp
Cho tứ diện SABCD có ABC là tam giác vuông cân tại A, đường cao SA Biết đường cao AH của tam giác ABC bằng a, góc giữa mặt phẳng (SBC) và mặt phẳng (ABC) bằng 60 ° .Tính theo a thể tích khối tứ diện SABC
A. a 3 6 3
B. a 3 3 3
C. 2 a 3 6 3
D. a 3 2 3
Cho tam giác ABC vuông tại A vẽ đường cao AH chia cạnh huyền BC thành hai đoạn thẳng BH20cm và CH45cm a)Chứng minh tam giác HBA đồng dạng với tam giác HAC b)Tính độ dài AHc)Tính diện tích tam giác ABC d)Cho AB10 căn 3 ,AC15 căn 3 .Gọi AD là đường phân giác trong của góc A và AH là đường cao .Tính tỉ số diện tích của tam giác ABC và tam giác ACD
Đọc tiếp
Cho tam giác ABC vuông tại A vẽ đường cao AH chia cạnh huyền BC thành hai đoạn thẳng BH=20cm và CH=45cm
a)Chứng minh tam giác HBA đồng dạng với tam giác HAC
b)Tính độ dài AH
c)Tính diện tích tam giác ABC
d)Cho AB=10 căn 3 ,AC=15 căn 3 .Gọi AD là đường phân giác trong của góc A và AH là đường cao .Tính tỉ số diện tích của tam giác ABC và tam giác ACD