Tính độ dài đường tròn ngoại tiếp Một hình vuông có cạnh là 4cm

Những câu hỏi liên quan
Tính độ dài đường tròn ngoại tiếp :
a) Một lục giác đều có cạnh là 4cm
b) Một hình vuông có cạnh là 4cm
c) Một tam giác đều có cạnh là 6cm
Tính độ dài đường tròn ngoại tiếp Một lục giác đều có cạnh là 4cm
Cạnh lục giác đều nội tiếp trong đường tròn (O;R) bằng bán kính R
Vì lục giác đều có cạnh bằng 4cm nên R =4cm
Độ dài đường tròn là C = 2πR=2π4=8π(cm)
Đúng 0
Bình luận (0)
a) Vẽ hình vuông cạnh 4cm.
b) Vẽ đường tròn ngoại tiếp hình vuông đó. Tính bán kính R của đường tròn này.
c) Vẽ đường tròn nội tiếp hình vuông đó. Tính bán kính r của đường tròn này.
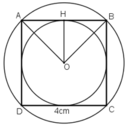
a) Vẽ hình vuông ABCD có cạnh 4cm.
b) Vẽ hai đường chéo AC và BD. Chúng cắt nhau tại O.
Đường tròn (O; OA) là đường tròn ngoại tiếp hình vuông ABCD.
Ta có:
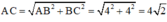 (cm)
(cm)
⇒ R = OA = AC/2 = 2√2 (cm).
c) Gọi H là trung điểm AB.
(O ; OH) là đường tròn nội tiếp hình vuông ABCD.
r = OH = AD/2 = 2cm.
Đúng 0
Bình luận (0)
1.Tính độ dài đường tròn ngoại tiếp
a) 1 lục giác đều có cạnh bằng 4 cm.
b) 1 hình vuông cạnh 4 cm
c) 1 tam giác đều cạnh 6 cm
2. Cho tam giác ABC cân có góc B=120°, AC bằng 6 cm. Tính độ dài đường tròn ngoại tiếp đó
Cho hình vuông có cạng là 4cm nội tiếp đường tròn (O). Hãy tính độ dài đường tròn (O) và diện tích hình tròn (O)
Cho hình vuông abcd gọi e là trung điểm cạnh ab biết bán kính đường tròn ngoại tiếp Tam giác edc bằng r tính độ dài các cạnh hình vuông abcd theo r
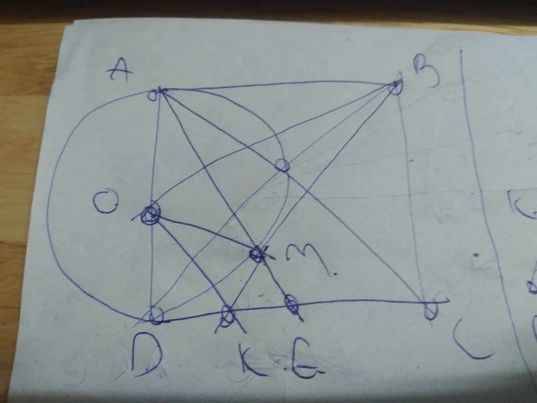
vẽ hình hộ mình đề này Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK A...
Đọc tiếp
vẽ hình hộ mình đề này Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK= AB^2/4 c) Đường thẳng AM cắt CD tại E. Cm K là trung điểm của ED và tính chu vi tứ giác ABKD
Tính độ dài đường tròn ngoại tiếp Một tam giác đều có cạnh là 6cm
trong tam giác đều ,giao điểm ba đường trung trực cũng là giao điểm của ba đường cao, ba đường trung tuyến .Do vậy bán kính của đường tròn ngoại tiếp bằng 2/3 đường trung tuyến của tam giác đều

Đúng 0
Bình luận (0)
Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK AB^2/4 c) Đường thẳng AM cắt CD tại E. Cm K là trung điểm của ED và tính chu vi tứ giác ABKD
Đọc tiếp
Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK= AB^2/4 c) Đường thẳng AM cắt CD tại E. Cm K là trung điểm của ED và tính chu vi tứ giác ABKD
a: Xét (O) có
AD là đường kính
AB\(\perp\)AD tại A
Do đó: AB là tiếp tuyến của (O)
Xét tứ giác AOMB có \(\widehat{OAB}+\widehat{OMB}=90^0+90^0=180^0\)
nên AOMB là tứ giác nội tiếp
=>A,O,M,B cùng thuộc một đường tròn
b: Xét (O) có
OD là bán kính
DK\(\perp\)DO tại D
Do đó: DK là tiếp tuyến của (O)
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: OB là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOB}\)
Xét (O) có
KM,KD là các tiếp tuyến
Do đó: OK là phân giác của góc DOM
=>\(\widehat{DOM}=2\cdot\widehat{KOM}\)
Ta có: \(\widehat{MOA}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{KOM}+\widehat{BOM}\right)=180^0\)
=>\(2\cdot\widehat{KOB}=180^0\)
=>\(\widehat{KOB}=90^0\)
=>OK\(\perp\)OB
Xét (O) có
BA,BM là các tiếp tuyến
Do đó: BA=BM
Xét (O) có
KD,KM là các tiếp tuyến
Do đó: KD=KM
Xét ΔOBK vuông tại O có OM là đường cao
nên \(BM\cdot MK=OM^2\)
=>\(BM\cdot MK=\left(\dfrac{1}{2}AD\right)^2=\dfrac{1}{4}AD^2=\dfrac{1}{4}AB^2\)
c: Ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
Ta có: OA=OM
=>O nằm trên đường trung trực của AM(2)
Từ (1) và (2) suy ra BO là đường trung trực của AM
=>BO\(\perp\)AM
mà BO\(\perp\)OK
nên AM//OK
Xét ΔDEA có
O là trung điểm của AD
OK//AE
Do đó: K là trung điểm của DE
Đúng 1
Bình luận (0)