Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
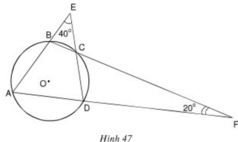
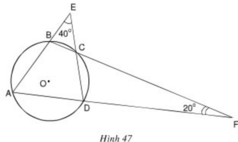
Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD.
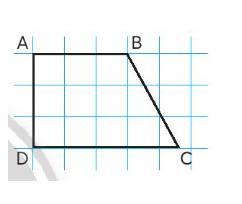
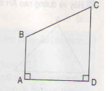
Cho hình tứ giác ABCD (xem hình bên).
a) Số đo mỗi góc của hình tứ giác là bao nhiêu độ?
b) Nêu tên các cặp cạnh vuông góc với nhau.
c) Nêu tên cặp cạnh song song với nhau.
a) Góc đỉnh A, cạnh AB, AD có số đo là 90o
Góc đỉnh D, cạnh DA, DC có số đo là 90o
Góc đỉnh B, cạnh BA, BC có số đo là 120o
Góc đỉnh C, cạnh CB, CD có số đo là 60o
b) AB và AD là cặp cạnh vuông góc với nhau
DA và DC là cặp cạnh vuông góc với nhau
c) AB và DC là cặp cạnh song song với nhau
Tính các góc của tứ giác ABCD biết các góc của nó lần lượt tỉ lệ với các số 5 ; 4 ; 5 ; 4. Hãy xem tứ giác ABCD có dạng đặc biệt nào? Vì sao?
Cho tứ giác ABCD biết số đo của các góc A, B, C, D tỉ lệ thuận với 1,2,3,4.
Tính số đo của các góc trong tứ giác ABCD.
Tứ giác ABCD có số đo góc A là 500, số đo góc D là 1300. Tứ giác ABCD là hình gì?
Bài 3:
a. Tính các góc của tứ giác ABCD bt số đo của chúng tương ứng với tỉ lệ với 2;2;1;1
b. Tứ giác ABCD cho ở câu a là hình gì? Vì sao?
( vẽ hình nữa nha)
a, Ta có \(\widehat{A}:\widehat{B}:\widehat{C}:\widehat{D}=2:2:1:1\Rightarrow\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{D}}{1}\) và \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
Áp dụng t/c dtsbn:
\(\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{1}=\dfrac{\widehat{D}}{1}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+1+2+2}=\dfrac{360^0}{6}=60^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=120^0\\\widehat{B}=120^0\\\widehat{C}=60^0\\\widehat{D}=60^0\end{matrix}\right.\)
b, Vì \(\widehat{A}+\widehat{C}=120^0+60^0=180^0\) mà 2 góc này ở vị trí TCP nên AB//CD
Do đó ABCD là hình thang
Vì \(\widehat{A}=\widehat{B}=120^0\) nên ABCD là hình thang cân
Tứ giác ABCD có số đo bốn góc A, B, C, D theo thứ tự lập thành cấp số cộng. Biết số đo góc C gấp 5 lần số đo góc A. Tính số đo các góc của tứ giác ABCD theo đơn vị độ.
Do A, B, C, D theo thứ tự lập thành một cấp số cộng nên ta có:
B = A + d; C = A + 2d; D = A + 3d.
Mặt khác: A + B + C + D = 360°
⇔ A + A + d + A + 2d + A + 3d = 360°
⇔ 4A + 6d = 360°
⇔ 2A + 3d = 180°
Ta lại có: A + 2d = 5A ⇔ d = 2A
⇒ 8A = 180°
⇒ A = 22,5° và d = 45°
⇒ B = 67,5°, C = 112,5°, D = 157,5°.
cho hình thang cân ABCD( AB // CD ) có góc A = 50 độ , C = 2 lần góc B tính số đo các góc của tứ giác ABCD
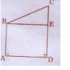
Cho hình tứ giác ABCD có góc đỉnh A và góc đỉnh D là các góc vuông
a) Hãy vẽ đường thẳng đi qua B và song song với cạnh AD, cắt cạnh DC tại điểm E.
b) Dùng ê ke kiểm tra xem góc đỉnh E của hình tứ giác BEDA có góc vuông hay không?
- Học sinh dùng ê – ke vẽ như hình dưới
- Học sinh dùng ê – ke để kiểm tra sẽ thấy góc đỉnh E của tứ giá BEDA là góc vuông
Nói thêm: Góc đỉnh B của tứ giác đó cũng là góc vuông. Tứ giác ABDA là hình chữ nhật