Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.
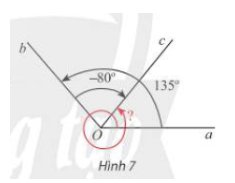
a, Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(135^o+n\cdot360^o,n\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(-80^o+m\cdot360^o,m\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(415^o+k\cdot360^o,k\in Z\)
b, \(\left(Oa,Ob\right)+\left(Ob,Oc\right)=135^o+n\cdot360^o+\left(-80^o\right)+m\cdot360^o\\ =55^o+\left(n+m\right)\cdot360^o\\ =415^o+\left(n+m-1\right)\cdot360^o\\ =415^o+k\cdot360^o=\left(Oa,Oc\right)\)
Với \(k=n+m-1;n,m,k\in Z\)
Trên đường tròn lượng giác, cho hai điểm M, M’ sao cho góc lượng giác \(\left( {OA,OM} \right) = \alpha ,\,\,\left( {OA,OM'} \right) = - \alpha \) (Hình 13)
a) Đối với hai điểm M, M’ nêu nhận xét về: hoành độ của chúng, tung độ của chúng.
b) Nêu mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)
a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)
Cho góc lượng giác ( OA; OB) có số đo bằng π/5. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác ( OA; O B) ?
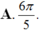
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0).
a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA; OA’), (OA, OB’) có số đo lần lượt là \(\pi \,\) và \( - \frac{\pi }{2}\)
Tham khảo:
a)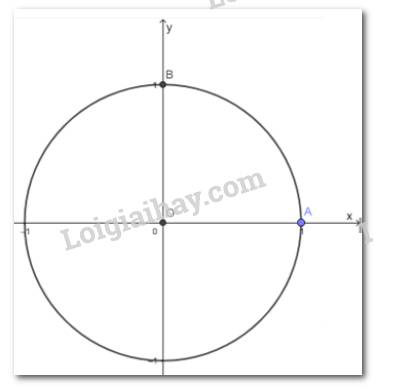 
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
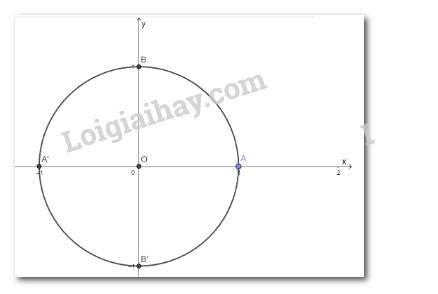
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = - 30^\circ \)
\(\begin{array}{l}\cos \left( { - 30^\circ } \right) = \frac{{\sqrt 3 }}{2} > 0\\\sin \left( { - 30^\circ } \right) = - \frac{1}{2} < 0\\\tan \left( { - 30^\circ } \right) = - \frac{{\sqrt 3 }}{3} < 0\\\cot \left( { - 30^\circ } \right) = - \sqrt 3 < 0\end{array}\)
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = \frac{{5\pi }}{6}\)
Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{6}} \right) < 0\\\sin \left( {\frac{{5\pi }}{6}} \right) > 0\\\tan \left( {\frac{{5\pi }}{6}} \right) < 0\\\cot \left( {\frac{{5\pi }}{6}} \right) < 0\end{array}\)
cho tam giấcbc vuông tại a, viết các tỉ số lượng giác của góc b và góc c. Có nhận xét gì về tỉ số lượng giác của 2 góc này
Xét ΔABC vuông tại A có
\(sinB=\dfrac{AC}{BC}\)
\(cosB=\dfrac{AB}{BC}\)
\(tanB=\dfrac{AC}{AB}\)
\(cotB=\dfrac{AB}{AC}\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
\(cosC=\dfrac{AC}{BC}\)
\(tanC=\dfrac{AB}{AC}\)
\(cotC=\dfrac{AC}{AB}\)
Nhận xét:
\(sinB=cosC\)
\(sinC=cosB\)
\(tanB=cotC\)
\(cotB=tanC\)
Gọi M, N, P là các điểm trên đường tròn lượng giác sao cho số đo của các góc lượng giác \(\left( {OA,OM} \right),\,\left( {OA,ON} \right),\,\left( {OA,OP} \right)\) lần lượt bằng \(\frac{\pi }{2};\,\,\frac{{7\pi }}{6};\,\, - \frac{\pi }{6}\). Chứng minh rằng tam giác MNP là tam giác đều.
Tham khảo:
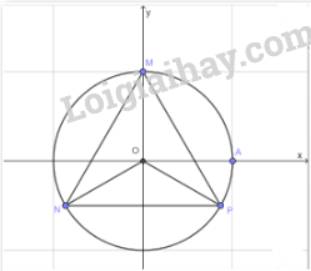
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều
Cho góc xOy , điểm A nằm trong góc xOy và cách đều hai cạnh Ox ; Oy .
CM : OA là phân giác của góc xOy và hãy rút ra 1 nhận xét .
Ta nối O với A.
Xét \(\Delta OAB\) và \(\Delta OAC\) có :
\(\hept{\begin{cases}\widehat{OBA}=\widehat{OCA=90^o}\\OAchung\\OB=OC\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta OAB=\Delta OAC\) ( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\widehat{BOA}=\widehat{COA}\)
\(\Rightarrow OA\) là tia phân giác của \(\widehat{xOy}\)
*) Nhận xét : Tập hợp các điểm cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó.
