Cho dãy số (Un) xác định bởi u 1 = 1 3 và u n + 1 = n + 1 3 n . u n . Tổng S = u 1 + u 2 2 + u 3 3 + . . . . . + u 10 10 bằng
![]()
![]()
![]()
![]()
Cho dãy số (Un) xác định bởi U1=-3 và U(n+1)=Un+ n^2 -3n +4, mọi n thuộc N*. Số 1391 là số hạng thứ mấy của dãy ?
Cho dãy số u n được xác định bởi u 1 = 2 u n + 1 = 4 u n + 9
Dãy số v n xác định bởi v n = u n + 3 , với mọi n ≥ 1 . Khẳng định nào dưới đây đúng?
A. Dãy v n là cấp số cộng với công sai d=3 .
B. Dãy v n là cấp số nhân với công bội q=4.
C. Dãy v n là cấp số cộng với công sai d=4 .
D. Dãy v n là cấp số nhân với công bội q= 9
Cho dãy số u n xác định bởi u 1 = 321 và u n + 1 = u n - 3 với mọi n ∈ N * . Tính tổng S của 125 số hạng đầu tiên của dãy số đó.
A. S = 16875
B. S = 63375
C. S = 63562,5
D. S = 16687,5
1) cho dãy số được xác định bởi
a) Tính
2) cho dãy số được xác định bởi
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
Cho dãy số ( u n ) xác định bởi u 1 = 3 và u n + 1 = u n + n , với mọi số nguyên dương n. Giá trị của u 1 + u 2 + u 3 bằng
A. 18
B. 13
C. 15
D. 16
Phương pháp:
Ứng với mỗi giá trị của n = 1, n = 2 ta tính các giá trị u2, u3 rồi tính giá trị của biểu thức.
Cách giải:
Ta có:
u n + 1 = u n + n , u 1 = 3
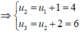
![]()
Chọn B
Cho dãy số u n xác định bởi u 1 = 5 và u n + 1 = 3 + u n . Số hạng tổng quát của dãy số này là:
A. u n = 8 + n
B. u n = 2 + 3 n
C. u n = 5 + 3 n
D. u n = 5 . 3 n
Chọn B.
- Ta có, u 1 = 5 và u n + 1 = 3 + u n nên dãy số là cấp số cộng với công sai d = 3, số hạng đầu u 1 = 5 .
- Do đó số hạng tổng quát của dãy số này là:
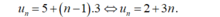
Cho dãy số u n xác định bởi u 1 = 321 u n + 1 = u n − 3 với mọi n ≥ 1 . Tổng của 125 số hạng đầu tiên của dãy số bằng:
A. 63375
B. 16687, 5
C. 16875
D. 63562, 5
Đáp án C
Với dãy số u n xác định như trên ta dễ thấy u n là cấp số cộng có số hạng đầu là u 1 = 321 công sai d = − 3 . Do đó, tổng của 125 số hạng đầu của u n là:
S 125 = 125. 2 u 1 + 125 − 1 d 2 = 125. 2.321 − 124.3 2 = 16875
Cho dãy số u n xác định bởi u 1 = 1 và u n + 1 = u n 2 + 2 , ∀ n ∈ N * . Tổng S = u 1 2 + u 2 2 + u 3 2 + . . . + u 1001 2 bằng
A. 1002001
B. 1001001
C. 1001002
D. 1002002
Đáp án A
Ta có u n + 1 2 = u n 2 + 2 = u n - 1 2 + 2 . 2 = u n - 2 2 + 2 . 3 = u 1 2 + 2 n
Do đó S = 1001 u 1 2 + 2 ( 0 + 1 + 2 + . . . + 1000 ) = 1001 + 2 . 1001 . 1000 2 = 1002001 .
Cho dãy số (Un) xác định bởi: { U1=1; Un+1=1/2un + 3/2; ∀n ϵ N*
Tình giới hạn của dãy số (Un)
Ai đó giúp em với, em cảm ơn rất nhiều ạ
Cho dãy số (Un) được xác định bởi: u1 = \(\dfrac{1}{3}\) và un+1 = \(\dfrac{2u_n}{2u_n\left(3n-1\right)+1}\), ∀n ∈ N*.
a) Tìm u4 và số hạng tổng quát un của dãy số.
b) Tính S = \(\dfrac{1}{u_1}+\dfrac{1}{u_2}+...+\dfrac{1}{u_n}\) (tổng gồm n số hạng) theo n.
Help me!!!
Gấp lắm ạ
Thank you so much!!!