Tính F x = ∫ sin 2 x 4 sin 2 x + 2 cos 2 x + 3 d x . Hãy chọn đáp án đúng.
![]()
![]()
![]()
![]()
1. Tìm x, biết:
a. \(\tan x+\cot x=2\)
b. \(\sin x.\cos x=\frac{\sqrt{3}}{4}\)
2.
a. Biết \(\tan\alpha=\frac{1}{3}\)Tính A=\(\frac{\sin\alpha-\cos\alpha}{\sin\alpha+\cos\alpha}\)
b. Biết \(\sin\alpha=\frac{2}{3}\)Tính B=\(3.\sin^2\alpha+4.\cos^2\alpha\)
c. Tính C=\(\sin^210^o+\sin^220^o+\sin^270^o+\sin^280^o\)
d. Tính D=\(\tan20^o.\tan35^o.\tan55^o.\tan70^o\)
e. Tính E=\(\sin^6\alpha+\cos^6\alpha+3.\sin^2\alpha.\cos^2\alpha\)
f. Tính F=\(3.\left(\sin^3\alpha+\cos^3\alpha\right)-2.\left(\sin^6\alpha+\cos^6\alpha\right)\)
g. Tính G=\(\sqrt{\sin^4\alpha+4.\cos^2\alpha}+\sqrt{\cos^4\alpha+4.\sin^2\alpha}\)
Mọi người giúp mình với. Mình cảm ơn ạ!
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Tìm số đo góc nhọn x:
a) \(4\sin x-1=1\)
b) \(2\sqrt{3}-3\tan x=\sqrt{3}\)
c) \(7\sin-3\cos\left(90^o-x\right)=2,5\)
d) \(\left(2\sin-\sqrt{2}\right)\left(4\cos-5\right)=0\)
e) \(\dfrac{1}{\cos^2x}-\tan x=1\)
f) \(\cos^2x-3\sin^2x=0,19\)
a) \(4sinx-1=1\Leftrightarrow4sinx=2\Leftrightarrow sinx=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow x=30^o\)
b) \(2\sqrt{3}-3tanx=\sqrt{3}\Leftrightarrow3tanx=2\sqrt{3}-\sqrt{3}=\sqrt{3}\Leftrightarrow tanx=\dfrac{\sqrt{3}}{3}\)
\(\Leftrightarrow x=30^o\)
c) \(7sinx-3cos\left(90^o-x\right)=2,5\Leftrightarrow7sinx-3sinx=2,5\Leftrightarrow4sinx=2,5\Leftrightarrow sinx=\dfrac{5}{8}\Leftrightarrow x=30^o41'\)
d)\(\left(2sin-\sqrt{2}\right)\left(4cos-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2sin-\sqrt{2}=0\\4cos-5=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}2sin=\sqrt{2}\\4cos=5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}sin=\dfrac{\sqrt{2}}{2}\\cos=\dfrac{5}{4}\left(loai\right)\end{matrix}\right.\)\(\Rightarrow x=45^o\)
Xin lỗi nãy đang làm thì bấm gửi, quên còn câu e, f nữa:"(
e) \(\dfrac{1}{cos^2x}-tanx=1\Leftrightarrow1+tan^2x-tanx-1=0\Leftrightarrow tan^2x-tanx=0\Leftrightarrow tanx\left(tanx-1\right)=0\Rightarrow tanx-1=0\Leftrightarrow tanx=1\Leftrightarrow x=45^o\)
f) \(cos^2x-3sin^2x=0,19\Leftrightarrow1-sin^2x-3sin^2x=0,19\Leftrightarrow1-4sin^2x=0,19\Leftrightarrow4sin^2x=0,81\Leftrightarrow sin^2x=\dfrac{81}{400}\Leftrightarrow sinx=\dfrac{9}{20}\Leftrightarrow x=26^o44'\)
Cho f(x)= log 5 ( sin x ) , x ∈ ( 0 ; π / 2 ) . Tính f'(x)
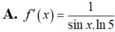
![]()
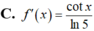
![]()
Tính
\(sin^4.x=\left(sin^2x\right)^2\)
a) A= \(\left(cos.x+sin.x\right)^2+\left(sin.x-cos.x\right)^2\)
b) B= \(sin^4.x-cos^4.x-2sin^2.x+1\)
c) C= \(2cos^4.x-sin^4.x+sin^2.x.cos^2.x+3sin^2.x\)
d) D= \(\left(cot.x+tan.x\right)^2-\left(cot.x-tan.x\right)^2\)
e) E= \(\sqrt{1+cos.x}.\sqrt{1-cosx}\)
f) F= \(sin.x\sqrt{1+tan^2x}\)
g) G= \(sin\left(180-x\right).cot\left(180-x\right)\)
h) H= \(cot.x\left(\frac{1+sin^2.x}{cos.x}-cos.x\right)\)
Chẹp ko hỉu đề boài :)
Chứng minh rằng \(f'\left(x\right)=0;\forall x\in R\) nếu :
a) \(f\left(x\right)=3\left(\sin^4x+\cos^4x\right)-2\left(\sin^6x+\cos^6x\right)\)
b) \(f\left(x\right)=\cos^6x+2\sin^4x.\cos^2x+3\sin^2x\cos^4x+\sin^4x\)
c) \(f\left(x\right)=\cos\left(x-\dfrac{\pi}{3}\right)\cos\left(x+\dfrac{\pi}{4}\right)+\cos\left(x+\dfrac{\pi}{6}\right)\cos\left(x+\dfrac{3\pi}{4}\right)\)
d) \(f\left(x\right)=\cos^2x+\cos^2\left(\dfrac{2\pi}{3}+x\right)+\cos^2\left(\dfrac{2\pi}{3}-x\right)\)
Chứng minh các biểu thức đã cho không phụ thuộc vào x.
Từ đó suy ra f'(x)=0
a) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
b) f(x)=1⇒f′(x)=0f(x)=1⇒f′(x)=0 ;
c) f(x)=\(\frac{1}{4}\)(\(\sqrt{2}\)-\(\sqrt{6}\))=>f'(x)=0
d,f(x)=\(\frac{3}{2}\)=>f'(x)=0
Giải các Phương trình sau
a) \(sin^4\frac{x}{2}+cos^4\frac{x}{2}=\frac{1}{2}\)
b) \(sin^6x+cos^6x=\frac{7}{16}\)
c) \(sin^6x+cos^6x=cos^22x+\frac{1}{4}\)
d) \(tanx=1-cos2x\)
e) \(tan(2x+\frac\pi3).tan(\frac\pi3-x)=1\)
f) \(tan(x-15^o).cot(x+15^o)=\frac{1}{3}\)
a.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{1}{2}\)
\(\Leftrightarrow2-\left(2sin\dfrac{x}{2}cos\dfrac{x}{2}\right)^2=1\)
\(\Leftrightarrow1-sin^2x=0\)
\(\Leftrightarrow cos^2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
b.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{7}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=\dfrac{7}{16}\)
\(\Leftrightarrow16-12.sin^22x=7\)
\(\Leftrightarrow3-4sin^22x=0\)
\(\Leftrightarrow3-2\left(1-cos4x\right)=0\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
c.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=cos^22x+\dfrac{1}{4}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=cos^22x+\dfrac{1}{4}\)
\(\Leftrightarrow3-3sin^22x=4cos^22x\)
\(\Leftrightarrow3=3\left(sin^22x+cos^22x\right)+cos^22x\)
\(\Leftrightarrow3=3+cos^22x\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
Chứng minh rằng: (Pls help me)
a, \(\frac{1}{\sin x}+\cot x=\cot\frac{x}{2}\)
b, \(\frac{1-\cos x}{\sin x}=\tan\frac{x}{2}\)
c,\(\tan\frac{x}{2}\left(\frac{1}{\cos x}+1\right)=\tan x\)
d,\(\frac{\sin2a}{2\cos a\left(1+\cos a\right)}=\tan\frac{a}{2}\)
e,\(\cot x+\tan\frac{x}{2}=\frac{1}{\sin x}\)
f,\(3-4\cos2x+\cos4x=8\sin^4x\)
g,\(\frac{1-\cos x}{\sin x}=\frac{\sin x}{1+\cos x}\)
h,\(\sin x+\cos x=\sqrt{2}\sin\left(x+\frac{\pi}{4}\right)\)
i,\(\sin x-\cos x=\sqrt{2}\sin\left(x-\frac{\pi}{4}\right)\)
l,\(\cos x-\sin x=\sqrt{2}\cos\left(x+\frac{\pi}{4}\right)\)
a/
\(\frac{1}{sinx}+\frac{cosx}{sinx}=\frac{1+cosx}{sinx}=\frac{1+2cos^2\frac{x}{2}-1}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{2cos^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{cos\frac{x}{2}}{sin\frac{x}{2}}=cot\frac{x}{2}\)
b/
\(\frac{1-cosx}{sinx}=\frac{1-\left(1-2sin^2\frac{x}{2}\right)}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{2sin^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}=\frac{sin\frac{x}{2}}{cos\frac{x}{2}}=tan\frac{x}{2}\)
c/
\(tan\frac{x}{2}\left(\frac{1}{cosx}+1\right)=\left(\frac{1-cosx}{sinx}\right)\left(\frac{1}{cosx}+1\right)=\frac{\left(1-cosx\right)\left(1+cosx\right)}{sinx.cosx}=\frac{1-cos^2x}{sinx.cosx}\)
\(=\frac{sin^2x}{sinx.cosx}=\frac{sinx}{cosx}=tanx\)
d/
\(\frac{sin2a}{2cosa\left(1+cosa\right)}=\frac{2sina.cosa}{2cosa\left(1+2cos^2\frac{a}{2}-1\right)}=\frac{sina}{2cos^2\frac{a}{2}}=\frac{2sin\frac{a}{2}cos\frac{a}{2}}{2cos^2\frac{a}{2}}=tan\frac{a}{2}\)
e/
\(cotx+tan\frac{x}{2}=\frac{cosx}{sin}+\frac{1-cosx}{sinx}=\frac{cosx+1-cosx}{sinx}=\frac{1}{sinx}\)
Các câu c, e đều sử dụng kết quả từ câu b
f/
\(3-4cos2x+cos4x=3-4cos2x+2cos^22x-1\)
\(=2cos^22x-4cos2x+2=2\left(cos^22x-2cos2x+1\right)\)
\(=2\left(cos2x-1\right)^2=2\left(1-2sin^2x-1\right)^2\)
\(=2.\left(-2sin^2x\right)^2=8sin^4x\)
g/
\(\frac{1-cosx}{sinx}=\frac{sinx\left(1-cosx\right)}{sin^2x}=\frac{sinx\left(1-cosx\right)}{1-cos^2x}=\frac{sinx\left(1-cosx\right)}{\left(1-cosx\right)\left(1+cosx\right)}=\frac{sinx}{1+cosx}\)
h/
\(sinx+cosx=\sqrt{2}\left(sinx.\frac{\sqrt{2}}{2}+cosx.\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(sinx.cos\frac{\pi}{4}+cosx.sin\frac{\pi}{4}\right)=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)\)
i/
\(sinx-cosx=\sqrt{2}\left(sinx.\frac{\sqrt{2}}{2}-cosx.\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(sinx.cos\frac{\pi}{4}-cosx.sin\frac{\pi}{4}\right)=\sqrt{2}sin\left(x-\frac{\pi}{4}\right)\)
j/
\(cosx-sinx=\sqrt{2}\left(cosx.\frac{\sqrt{2}}{2}-sinx\frac{\sqrt{2}}{2}\right)\)
\(=\sqrt{2}\left(cosx.cos\frac{\pi}{4}-sinx.sin\frac{\pi}{4}\right)=\sqrt{2}cos\left(x+\frac{\pi}{4}\right)\)
Cho \(\sin x+\cos x=m\). Tính theo m các biểu thức sau:
1) \(A=\sin^2x+\cos^2x\)
2) \(B=\sin^3x+\cos^3x\)
3) \(C=\sin^4x+\cos^4x\)
4) \(D=\sin^6x+\cos^6x\)
\(sinx+cosx=m\Leftrightarrow\left(sinx+cosx\right)^2=m^2\)
\(\Leftrightarrow1+2sinx.cosx=m^2\Rightarrow sinx.cosx=\dfrac{m^2-1}{2}\)
\(A=sin^2x+cos^2x=1\)
\(B=sin^3x+cos^3x=\left(sinx+cosx\right)^3-3sinx.cosx\left(sinx+cosx\right)\)
\(=m^3-\dfrac{3m\left(m^2-1\right)}{2}=\dfrac{2m^3-3m^3+3m}{2}=\dfrac{3m-m^3}{2}\)
\(C=\left(sin^2+cos^2x\right)^2-2\left(sinx.cosx\right)^2=1-2\left(\dfrac{m^2-1}{2}\right)^2\)
\(D=\left(sin^2x\right)^3+\left(cos^2x\right)^3=\left(sin^2x+cos^2x\right)^3-3\left(sin^2x+cos^2x\right)\left(sinx.cosx\right)^2\)
\(=1-3\left(\dfrac{m^2-1}{2}\right)^2\)
Cho \(\cos2x=\dfrac{1}{2}\). Tính giá trị biểu thức:
\(P=\sin^22x-4\left(sin\dfrac{x}{2}.cos^5\dfrac{x}{2}-sin^5\dfrac{x}{2}.cos\dfrac{x}{2}\right)^2\)
Help me!!!!! plsssss
\(P=sin^22x-\left[2sin\dfrac{x}{2}cos\dfrac{x}{2}\left(cos^4\dfrac{x}{2}-sin^4\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx\left(cos^2\dfrac{x}{2}-sin^2\dfrac{x}{2}\right)\left(cos^2\dfrac{x}{2}+sin^2\dfrac{x}{2}\right)\right]^2\)
\(=sin^22x-\left[sinx.cosx.1\right]^2\)
\(=sin^22x-\left[\dfrac{1}{2}sin2x\right]^2\)
\(=\dfrac{3}{4}sin^22x=\dfrac{3}{4}\left(1-cos^22x\right)=\dfrac{3}{4}\left(1-\dfrac{1}{4}\right)=\dfrac{9}{16}\)