Tam giác ABC có A ^ = 45 o ; B ^ - C ^ = 35 o . Trên tia đối của tia AC lấy điểm E sao cho AE=AB. Tính số đo góc CBE
A. 107 °
B. 107 ° 30'
C. 108 °
D. 100 °
Cho tam giác ABC có , C = 45o, BC = a. Hãy tính AB, AC và diện tích
tam giác ABC.
Cho tam giác ABC có \(\stackrel\frown{B}\) = \(75^o\), \(\stackrel\frown{C}=45^o\) và BC = 50.
a) Tính độ dài cạnh AB.
b) Tính diện tích tam giác ABC.
c) Tính đường cao xuất phát từ đỉnh A của tam giác ABC
a: Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{A}=180^0-75^0-45^0=60^0\)
Xét ΔABC có
\(\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\)
=>\(\dfrac{AB}{sin45}=\dfrac{50}{sin60}\)
=>\(AB\simeq40,82\)
b: \(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC\cdot sinABC=\dfrac{1}{2}\cdot40,82\cdot50\cdot sin75\simeq985,73\)
c: Độ dài đường cao xuất phát từ A là:
\(2\cdot\dfrac{985.73}{50}=39,4292\left(\right)\)
tam giác ABC có A=\(75^o\), B=\(45^o\), AC=2. tính cạnh AB.
góc C=180-75-45=60 độ
Xét ΔABC có AB/sinC=AC/sinB
=>AB/sin60=2/sin45
=>\(AB=\sqrt{6}\)
Ta có:
\(\widehat{C}=180^o-75^o-45^o=60^o\)
Xét tam giác ABC ta có:
\(\dfrac{AB}{sinC}=\dfrac{AC}{sinB}\)
\(\Rightarrow AB=\dfrac{ACsinC}{sinB}\)
\(\Rightarrow AB=\dfrac{2\cdot sin60^o}{sin45^o}\)
\(\Rightarrow AB=\sqrt{6}\)
Vậy: ...
Cho tam giác ABC có AB = 12; \(\widehat B = {60^o}\); \(\widehat C = {45^o}\). Tính diện tích của tam giác ABC.
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {60^o}.\frac{{12}}{{\sin {{45}^o}}} = 6\sqrt 6 \)
Lại có: \(\widehat A = {180^o} - ({60^o} + {45^o}) = {75^o}\)
\( \Rightarrow \)Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.12.6\sqrt 6 .\sin {75^o} \approx 85,2\)
Vậy diện tích tam giác ABC là 85,2.
Cho tam giác ABC vuông tại A có góc B > 45o
1, Chứng Minh C < 45o
2, So sánh các cạnh của tam giác ABC
a) Xét tam giác vuông ABC tại A có:
\(\widehat{B}+\widehat{C}=180^o-\widehat{A}=180^o-90^o=90^o\)
Mà \(\widehat{B}>45^o\Leftrightarrow\widehat{C}< 90^o-45^o\Rightarrow\widehat{C}< 45^o\)(đpcm)
b) Áp dụng mối quan hệ giữa góc và cạnh trong tam giác, ta thấy:
- Do \(\widehat{C}< 45^o< \widehat{B}\Leftrightarrow AB< AC\)
- Do \(\widehat{A}=90^o\Leftrightarrow\widehat{C}< \widehat{B}< \widehat{A}\Leftrightarrow AB< AC< BC\)
Cho tam giác ABC có \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\). Tính R,b,c.
Áp dụng định lí sin trong tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\( \Rightarrow R = \dfrac{a}{{2\sin A}};\;\;b = \dfrac{{a.\sin B}}{{\sin A}}\)
Mà \(a = 10,\widehat A = {45^o},\widehat B = {70^o}\)
\( \Rightarrow R = \dfrac{{10}}{{2\sin {{45}^o}}} = 5\sqrt 2 ;\;\;b = \dfrac{{a.\sin {{70}^o}}}{{\sin {{45}^o}}} \approx 13,29\)
Mặt khác: \(\widehat A = {45^o},\widehat B = {70^o} \Rightarrow \widehat C = {65^o}\)
Từ định lí sin ta suy ra: \(c = \dfrac{{a.\sin C}}{{\sin A}} = \dfrac{{10.\sin {{65}^o}}}{{\sin {{45}^o}}} \approx 12,82.\)
Vậy \(R = 5\sqrt 2 ;\;\;b \approx 13,29\); \(c \approx 12,82.\)
Cho tam giác ABC có BC = 4cm, \(\widehat{B}=70^o\), \(\widehat{C}=45^o\). Tính độ dài AC và diện tích tam giác ABC?
Kẻ đường cao AH ứng với BC, đặt \(CH=x\Rightarrow BH=4-x\)
Trong tam giác vuông ABH
\(tanB=\dfrac{AH}{BH}\Rightarrow AH=BH.tanB=\left(4-x\right).tan70^0\)
Trong tam giác vuông ACH:
\(tanC=\dfrac{AH}{CH}\Rightarrow AH=CH.tanC=x.tan45^0=x\)
\(\Rightarrow\left(4-x\right)tan70^0=x\)
\(\Leftrightarrow\left(1+tan70^0\right)x=4.tan70^0\)
\(\Leftrightarrow x=\dfrac{4tan70^0}{1+tan70^0}\approx2,2\left(cm\right)\)
\(\Rightarrow CH=AH=2,2\left(cm\right)\)
\(AC=\sqrt{CH^2+AH^2}=AH\sqrt{2}\approx3,1\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.2,2.4=4,4\left(cm^2\right)\)
Cho tam giác ABC có \(\widehat B = {60^o},\;\,\widehat C = {45^o},AC = 10\). Tính \(a,R,S,r\).
Theo định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\quad (*)\)
+) Ta có: \(\hat A = {180^o} - \left( {\hat B + \;\hat C} \right) = {180^o} - \left( {{{60}^o} + {{45}^o}} \right) = {75^o}\)
\( \Rightarrow a = \frac{b}{{\sin B}}.\sin A = \frac{{10}}{{\sin {{60}^o}}}.\sin {75^o} \approx 11,154\)
+) \((*) \Rightarrow R = \frac{b}{{2\sin B}} = \frac{{10}}{{2\sin {{60}^o}}} = \frac{{10}}{{2.\frac{{\sqrt 3 }}{2}}} = \frac{{10\sqrt 3 }}{3}.\)
+) Diện tích tam giác ABC là: \(S = \frac{1}{2}ab.\sin {\mkern 1mu} \hat C\) \( \approx \frac{1}{2}.11,154.10.\sin {45^o}\)\( \approx 39,44\)
+) Lại có: \(R = \frac{c}{{2\sin C}}\)\( \Rightarrow c = 2.\frac{{10\sqrt 3 }}{3}.\sin {45^o} = \frac{{10\sqrt 6 }}{3} \approx 8,165\)
\( \Rightarrow p = \frac{{a + b + c}}{2} \approx \frac{{11,154 + 10 + 8,165}}{2} \approx 14,66\)
\( \Rightarrow r = \frac{S}{p} \approx \frac{{39,44}}{{14,66}} \approx 2,7\)
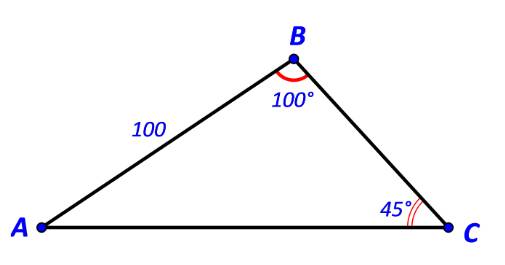
Cho tam giác ABC có \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
Cho tam giác ABC cân tại A có BAC=45o,AB=a . Tính BC theo a
Kẻ đường cao sau đó dùng ht giữa cạnh và góc là ra
Kẻ đường cao AH ta có: góc BAH = góc CAH = 22 độ 30 phút.
\(BC=BH+CH=2a.\sin22^030'=a.\frac{2-\sqrt{2}}{2}\)