Cho đường thẳng Δ có phương trình 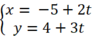 và vectơ n→ = (3; -2). Hãy chứng tỏ n→ vuông góc với vectơ chỉ phương của Δ.
và vectơ n→ = (3; -2). Hãy chứng tỏ n→ vuông góc với vectơ chỉ phương của Δ.

Những câu hỏi liên quan
Đường thẳng Δ đi qua M(x0;y0) và nhận vectơ
n
→
a
;
b
làm vectơ pháp tuyến có phương trình là: A. a(x - y0) + b(y - x0) 0 B. b(x - x0) + a(y - y0) 0 C. a(x + x0) + b(y + y0) 0 D. a(x - x0) + b(y - y0) 0
Đọc tiếp
Đường thẳng Δ đi qua M(x0;y0) và nhận vectơ n → = a ; b làm vectơ pháp tuyến có phương trình là:
A. a(x - y0) + b(y - x0) = 0
B. b(x - x0) + a(y - y0) = 0
C. a(x + x0) + b(y + y0) = 0
D. a(x - x0) + b(y - y0) = 0
Chọn D.
Phương trình tổng quát của đường thẳng Δ đi qua M(x0;y0) nhận 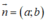 là VTPT là: a.(x - x0) + b.(y - y0) = 0
là VTPT là: a.(x - x0) + b.(y - y0) = 0
Đúng 0
Bình luận (0)
Phương trình tham số của đường thẳng Δ đi qua M(1;-3) và nhận vectơ
n
→
1
;
2
làm vectơ pháp tuyến. A.
∆
:
x
+
2
y
+
5
0
B.
∆
:
x
1
+...
Đọc tiếp
Phương trình tham số của đường thẳng Δ đi qua M(1;-3) và nhận vectơ n → 1 ; 2 làm vectơ pháp tuyến.
A. ∆ : x + 2 y + 5 = 0
B. ∆ : x = 1 + t y = - 3 + 2 t
C. ∆ : x = 1 - 2 t y = - 3 + t
D. ∆ : x - 1 - 2 = y + 3 1
Chọn C.
Vì Δ nhận vectơ n → 1 ; 2 làm vectơ pháp tuyến nên VTCP của Δ là u → - 2 ; 1
Vậy phương trình tham số của đường thẳng Δ là
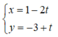
Đúng 0
Bình luận (0)
Cho đường thẳng Δ có phương trình tổng quát: 2x-3y+ 12 0. Vectơ nào sau đây không là vectơ chỉ phương của Δ
Đọc tiếp
Cho đường thẳng Δ có phương trình tổng quát: 2x-3y+ 12= 0. Vectơ nào sau đây không là vectơ chỉ phương của Δ
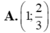
![]()
![]()
![]()
Cho điểm A(-1; 2; -3), vectơ
a
→
(6; -2; -3) và đường thẳng d có phương trình:
x
1
+
3
t
y
-
1
+
2...
Đọc tiếp
Cho điểm A(-1; 2; -3), vectơ a → = (6; -2; -3) và đường thẳng d có phương trình: x = 1 + 3 t y = - 1 + 2 t z = 3 - 5 t Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc với a → và cắt đường thẳng d.
(α) ⊥ a →
Δ ⊥ a →
⇒ Δ song song hoặc nằm trong (α).
Mà Δ và (α) cùng đi qua A
⇒ Δ ⊂ (α)
Δ cắt d ⇒ Δ cắt d tại M
⇒ Δ chính là đường thẳng AM.
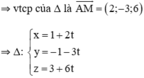
Đúng 0
Bình luận (0)
Đường thẳng Δ đi qua M(x0; y0) và nhận vectơ làm vectơ chỉ phương có phương trình là: A.
x
x
0
+
d
t
y
y
0
+...
Đọc tiếp
Đường thẳng Δ đi qua M(x0; y0) và nhận vectơ 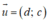 làm vectơ chỉ phương có phương trình là:
làm vectơ chỉ phương có phương trình là:
A. x = x 0 + d t y = y 0 + c t
B. x = x 0 - c t y = y 0 + d t
C. x = x 0 + c t y = y 0 + d t
D. x = x 0 + d t y = y 0 - c t
Chọn A.
Phương trình tham số của đường thẳng Δ là:
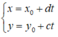
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x -3 + 2t, y 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 0.a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
Đọc tiếp
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
A nhé
hihhihihiihihihhiihhiihihihih
Trong không gian Oxyz, cho đường thẳng
d
:
x
1
+
3
t
y
1
+
4
t
z...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d : x = 1 + 3 t y = 1 + 4 t z = 1 . Gọi Δ là đường thẳng đi qua điểm A 1 ; 1 ; 1 và có vectơ chỉ phương u → = 1 ; - 2 ; 2 . Đường phân giác của góc nhọn tạo bởi d và Δ có phương trình là
A. x = 1 + 7 t y = 1 + t z = 1 + 5 t
B. x = - 1 + 2 t y = - 10 + 11 t z = - 6 - 5 t
C. x = - 1 + 2 t y = - 10 + 11 t z = 6 - 5 t
D. x = 1 + 3 t y = 1 + 4 t z = 1 - 5 t
Chọn đáp án C.

nên một vectơ chỉ phương của đường phân giác của góc nhọn tạo bởi d và Δ là
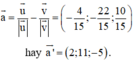
Nhận thấy tọa độ điểm A thỏa mãn phương trình ở phương án C nên phương án đúng là C.
Cách 2: Đường thẳng d và đường thẳng Δ có vectơ chỉ phương lần lượt là
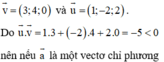
của đường phân giác của góc nhọn tạo bởi d và Δ thì
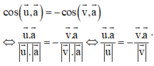
Kiểm tra từng phương án đến khi tìm được phương án đúng.
Tọa độ của điểm A không thỏa mãn phương trình ở phương án B nên loại phương án này.
- Phương án A: Đường thẳng có vectơ chỉ phương ![]()

Đúng 0
Bình luận (0)
Cho đường thẳng Δ có phương trình tham số:a) Vectơ chỉ phương của đường thẳng là:a (1; -2) b (2; 1) c (1; 1) d (-1; -2)b) Điểm nào trong các điểm sau thuộc Δ:A. (1; 3) B. (1; -5) C. (0; 1) D. (2; 1)c) Với t 4 ta có điểm nào sau đây thuộc Δ:A. (6; 7) B. (-7; 6) C. (6; -7) D. (6; 9)
Đọc tiếp
Cho đường thẳng Δ có phương trình tham số:
a) Vectơ chỉ phương của đường thẳng là:
a = (1; -2) b = (2; 1) c = (1; 1) d = (-1; -2)
b) Điểm nào trong các điểm sau thuộc Δ:
A. (1; 3) B. (1; -5) C. (0; 1) D. (2; 1)
c) Với t = 4 ta có điểm nào sau đây thuộc Δ:
A. (6; 7) B. (-7; 6) C. (6; -7) D. (6; 9)
Cho đường thẳng Δ có phương trình tham số:
a) Vectơ chỉ phương của đường thẳng là:
a = (1; -2) b = (2; 1) c = (1; 1) d = (-1; -2)
b) Điểm nào trong các điểm sau thuộc Δ:
A. (1; 3) B. (1; -5) C. (0; 1) D. (2; 1)
c) Với t = 4 ta có điểm nào sau đây thuộc Δ:
A. (6; 7) B. (-7; 6) C. (6; -7) D. (6; 9)
Đúng 1
Bình luận (0)
Đường thẳng d có một vectơ pháp tuyến là
n
→
-
2
;
-
5
. Đường thẳng Δ vuông góc với d có một vectơ chỉ phương là: A.
u
1
→
(
5
;
-
2
)
B.
u...
Đọc tiếp
Đường thẳng d có một vectơ pháp tuyến là n → = - 2 ; - 5 . Đường thẳng Δ vuông góc với d có một vectơ chỉ phương là:
A. u 1 → = ( 5 ; - 2 )
B. u 2 → = ( - 5 ; 2 )
C. u 3 → = ( 2 ; 5 )
D. u 4 → = ( 2 ; - 5 )
Chọn C.
Đường thẳng Δ vuông góc với d nhận VTPT của d là VTCP
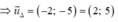
Đúng 0
Bình luận (0)








