Chọn D.
Phương trình tổng quát của đường thẳng Δ đi qua M(x0;y0) nhận 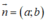 là VTPT là: a.(x - x0) + b.(y - y0) = 0
là VTPT là: a.(x - x0) + b.(y - y0) = 0
Chọn D.
Phương trình tổng quát của đường thẳng Δ đi qua M(x0;y0) nhận 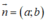 là VTPT là: a.(x - x0) + b.(y - y0) = 0
là VTPT là: a.(x - x0) + b.(y - y0) = 0
Phương trình của đường thẳng qua điểm M(x0;y0 ) có vectơ pháp tuyến n → = a ; b là:
A. x − x 0 a = y − y 0 b
B. b x − x 0 − a y − y 0 = 0
C. a x + x 0 + b y + y 0 = 0
D. a x - x 0 + b y - y 0 = 0
Đường thẳng Δ đi qua M(x0; y0) và nhận vectơ 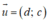 làm vectơ chỉ phương có phương trình là:
làm vectơ chỉ phương có phương trình là:
A. x = x 0 + d t y = y 0 + c t
B. x = x 0 - c t y = y 0 + d t
C. x = x 0 + c t y = y 0 + d t
D. x = x 0 + d t y = y 0 - c t
Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M 0 ( x 0 ; y 0 ; z 0 ) và có vectơ chỉ phương là u → , với a, b, c khác 0. Trong các khẳng định sau, khẳng định nào sai?
A. Phương trình chính tắc của đường thẳng d là: 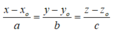
B. Phương trình tham số của đường thẳng d là: x = x 0 + at , y = y 0 + bt , z = z 0 + ct
C. Đường thẳng d nằm trong hai mặt phẳng :(P): b( x - x 0 ) - a ( y - y 0 ) = 0 và (Q): c ( x - x 0 ) - a ( z - z 0 ) = 0
D. Phương trình đường thẳng d là: a ( x - x 0 ) + b ( y - y 0 ) + c ( z - z 0 ) = 0
Cho đường tròn (C) có phương trình x − a 2 + y − b 2 = R 2 và điểm M ( x 0 ; y 0 ) nằm bên trong đường tròn. Đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB. Phương trình của ∆ là:
A. ( a - x 0 ) ( x - x 0 ) + ( b - y 0 ) ( y - y 0 ) = 0
B. a + x 0 x − x 0 + b + y 0 y − y 0 = 0
C. ( a - x 0 ) ( x + x 0 ) + ( b - y 0 ) ( y + y 0 ) = 0
D. a + x 0 x + x 0 + b + y 0 y + y 0 = 0
Khoảng cách từ điểm M(x0;y0) đường thẳng Δ: ax + by + c = 0 là:
A. d ( M , ∆ ) = a . x 0 + b . y 0 + c a + b
B. d ( M , ∆ ) = a . x 0 + b . y 0 + c a 2 + b 2
C. d ( M , ∆ ) = a . x 0 + b . y 0 a 2 + b 2
D. d ( M , ∆ ) = a . x 0 + b . y 0 + c a 2 + b 2
cho hàm số y=x2-5x+8 có đồ thị là (P) và hai điểm A(4,-1) , B(10,5) . biết điểm M(x0,y0) trên (P) thỏa mãn diện tích tam giác MAB nhỏ nhất . tính tổng x0 + y0
Hệ phương trình 2 x + y 2 − 5 4 x 2 − y 2 + 6 4 x 2 − 4 x y + y 2 = 0 2 x + y + 1 2 x − y = 3 nghiệm x 0 ; y 0 thỏa mãn x 0 > 1 2 . Khi đó P = x 0 + y 0 2 có giá trị là:
A. 1
B. 7 16
C. 3
D. 1 hoặc 7 16
Trong mặt phẳng Oxy, cho điểm A(2;-4), đường thẳng Δ: x = -3 + 2t, y = 1 + t và đường tròn (C): x^2 + y^2 – 2x – 8y – 8 = 0.
a. Tìm một vectơ pháp tuyến n của đường thẳng Δ. Lập phương trình tổng quát của đường thẳng d, biết d đi qua điểm A và nhận n làm vectơ pháp tuyến.
b. Viết phương trình đường tròn (T), biết (T) có tâm A và tiếp xúc với Δ.
c. Gọi P, Q là các giao điểm của Δ và (C). Tìm toạ độ điểm M thuộc (C) sao cho tam giác MPQ cân tại M.
Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?
A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.
B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x).
C. Số M = f( x 0 ) trong đó x 0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D
D. Nếu tồn tại x 0 ∈ D sao cho M = f( x 0 ) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.