Chọn B.
Khoảng cách từ điểm M(x0;y0)đường thẳng Δ: ax + by + c = 0 được tính theo công thức:
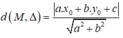
Chọn B.
Khoảng cách từ điểm M(x0;y0)đường thẳng Δ: ax + by + c = 0 được tính theo công thức:
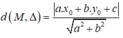
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau:
a, A(3; 5) và Δ : 4x + 3y +1 = 0
b, B(1; -2) và d: 3x – 4y -26 = 0
c, C(1; 2) và m: 3x + 4y -11 = 0
Trong mặt phẳng Oxy, (C) tâm I bán kính R = 2. Lấy M trên đường thẳng d: x+y=0. Từ M kẻ 2 tiếp tuyến MA,MB đến (C) ( A, B là tiếp điểm). Biết phương trình đường thẳng AB: 3x+y-2=0 và khoảng cách từ tâm I đến d = 2 căn 2 . Viết ptrinh đường tròn (C)
cho đường thẳng Δ : x + y - 2 = 0 và điểm A( 2; 2). Tìm tọa độ điểm M thuộc đường thẳng Δ sao cho khoảng cách từ A đến M nhỏ nhất.
Bài 1: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua đường thẳng Δ, với:
a, d: 2x-y+1=0, Δ: 3x-4y+2=0
b, d: x-2y+4=0, Δ: 2x+y-2=0
c, d: x+y-1=0, Δ: x-3y+3=0
d, d: 2x-3y+1=0, Δ: 2x-3y-1=0
Bài 2: Lập phương trình đường thẳng d' đối xứng với đường thẳng d qua điểm I với:
a, d: 2x-y+1=0, I(2;1)
b, d: x-2y+4=0, I(-3;0)
c, d: x+y-1=0, I(0:3)
d, d: 2x-3y+1=0, I trùng O(0;0)
GIÚP EM VỚI Ạ!! EM ĐANG CẦN GẤP LẮM HUHUU T^T EM XIN CẢM ƠN!!!
Trong mặt phẳng Oxy, cho ba điểm A(-3;5),B(4;6)
a.Viết phương trình đường thẳng qua 2 điểm A,B
b.Viết phương trình d qua A và song song (d1): 3x-y+5=0
c.Tìm M trên (d1) sao cho khoảng cách từ M đến (Δ): x-2y+5=0 là 2\(\sqrt{5}\)
d.Viết phương trình (d2) qua C(3;1) và cách đều A,B
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
a)Viết phương trình đường tròn đi qua 3 điểm A(-1;1);B(3;1);C(1;3)
b)Cho (C):x2+y2-4x+6y+3=0 và (Δ):3x-y+m=0.Tìm m để đường thẳng (Δ) tiếp xúc với đường tròn (C)
1) Nếu bất phương trình /2x-1/ < /1-x/ có tập nghiệm S=(0;a) thì a thuộc khoảng
2)Biết đường thẳng ax+by-3=0, a,b thuộc Z đi qua điểm M(1;1) và tạo với đường thẳng d: 3x-y+7=0 một góc 45 độ. Khi đó a-b bằng?
Trong không gian Oxyz, cho hai điểm A(-2; -2; -4), M(1; 0; 0). Lập phương trình đường thẳng d đi qua điểm M, nằm trong mặt phẳng (P): x + y + z - 1 = 0 sao cho khoảng cách từ A đến đường thẳng d đạt giá trị lớn nhất
A. d : x - 1 - 2 = y 1 = z 1
B. d : x - 1 3 = y 2 = z 4
C. d : x + 1 2 = y 1 = z 1
D. d : x - 1 1 = y 1 = z 1