Điểm O(0;0) thuộc miền nghiệm của bất phương trình nào sau đây?
A. x + 3y + 2 ≤ 0
B. x + y + 2 ≤ 0
C. 2 x + 5 y - 2 ≥ 0
D. 2 x + y + 2 ≥ 0
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
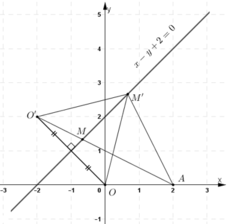
a, Cách 1: Gọi O’ là điểm đối xứng với O qua (Δ)
⇒ OO’ ⊥ Δ tại trung điểm I của OO’.
+ (Δ) nhận 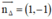 là một vtpt ⇒ (Δ) nhận
là một vtpt ⇒ (Δ) nhận 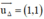 là một vtcp
là một vtcp
OO’ ⊥ Δ ⇒ OO’ nhận 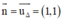 là một vtpt. Mà O(0, 0) ∈ OO’
là một vtpt. Mà O(0, 0) ∈ OO’
⇒ Phương trình đường thẳng OO’: x + y = 0.
+ I là giao OO’ và Δ nên tọa độ của I là nghiệm của hệ phương trình:
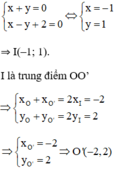
Cách 2: Gọi O’(x, y) là điểm đối xứng với O qua Δ.
+ Trung điểm I của OO’ là 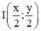
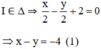
+ (Δ) nhận 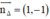 là một vtpt ⇒ (Δ) nhận
là một vtpt ⇒ (Δ) nhận 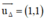 là một vtcp.
là một vtcp.
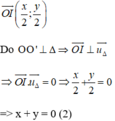
Từ (1) và (2) ta có hệ phương trình
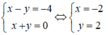
Vậy O’(–2; 2).
b)
+ Vì O và A nằm cùng một nửa mặt phẳng bờ là đường thẳng Δ nên đoạn thẳng OA không cắt Δ.
O’ và A thuộc hai nửa mặt phẳng khác nhau bờ là đường thẳng Δ nên O’A cắt Δ.
Do O’ đối xứng với O qua đường thẳng ∆ nên ∆ là đường trung trực của đoạn thẳng OO’, với mọi M ∈ Δ ta có MO = MO’.
Độ dài đường gấp khúc OMA bằng OM + MA = O’M + MA ≥ O’A.
⇒ O’M + MA ngắn nhất khi O’M + MA = O’A ⇔ M là giao điểm của O’A và Δ.
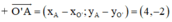
⇒ O’A nhận 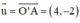 là một vtcp
là một vtcp
⇒ O’A nhận 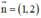 là một vtpt. Mà A(2; 0) ∈ O’A
là một vtpt. Mà A(2; 0) ∈ O’A
⇒ Phương trình đường thẳng O’A : 1(x - 2) + 2(y - 0)= 0 hay x + 2y – 2 = 0.
M là giao điểm của O’A và Δ nên tọa độ điểm M là nghiệm của hệ :
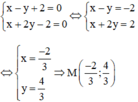
Vậy điểm M cần tìm là 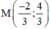
Cho các điểm A(-1; 0), B(0; 2), C(2; -3), D(3; 0), O(0; 0). Có bao nhiêu điểm nằm trên trục hoành trong số các điểm trên?
A. 0
B. 1
C. 2
D. 3
Các điểm nằm trên trục hoành là các điểm có tung độ bằng 0. Trong số các điểm ở trên ta thấy những điểm có tung độ bằng 0 là: A(-1; 0), D(3; 0), O(0; 0) . Vậy có ba điểm nằm trên trục hoành
Chọn đáp án D
Cho các điểm A(-1; 2), B(-2; 1), C(2; -3), D(2; 0), O(0; 0). Có bao nhiêu điểm nằm trong góc phần tư thứ 2 trong số các điểm trên?
A. 0
B. 1
C. 2
D. 3
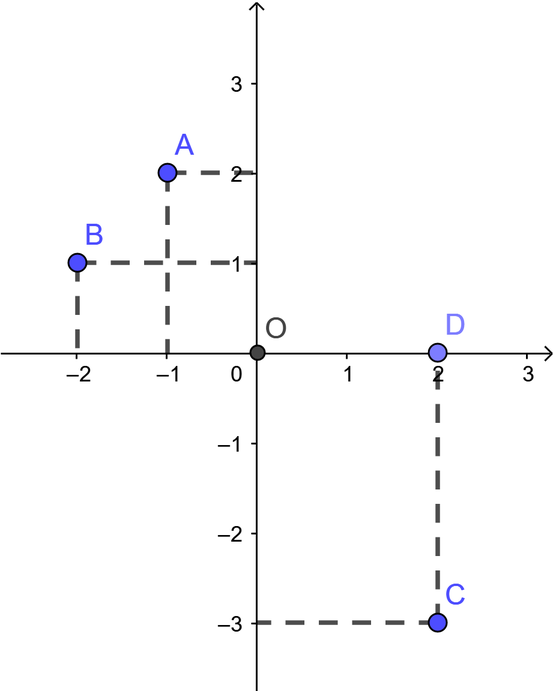
Biểu diễn các điểm trên hệ trục tọa độ Oxy ta thấy có hai điểm nằm trong góc phần tư thứ hai là A và B
Chọn đáp án C
Cho tam giác ABC có ba góc nhọn. Gọi O là trung điểm của BC. Gọi D là điểm đối xứng của A qua BC; E là điểm đối xứng của A qua O.
Đề yêu cầu CMR : BCED là hình thang cân ??
Ta có : A đối xứng D qua BC , gọi AD cắt BC tại H ta có AD \(\perp\) BC tại H và AH = HD
Xét tg ADE ta có ; AH = HD , AO = OE
=> OH // DE hay BC // DE .
tứ giác BCED có BC//DE => BCED là hih thang .
Xét tg OAB và tg OEC có :
OB = OC , OA = OE , góc AOB = góc COE
=> tg OAB = tg OEC => góc ABO = góc OCE (1).
Có : BH \(\perp\) AD tại trung điểm H của AD
=> BAD cân tại B => góc ABH = góc HBD (2) .
Từ (1) và (2) có : góc HBD = góc OCE
=> hih thang BCED có : góc HBD = góc OCE
=> BCED là hih thang cân .
Xem thêm tại : Câu hỏi của Quang Trần - Toán lớp 8 | Học trực tuyến ( https://h.vn/hoi-dap/question/674960.html )
Gợi ý cho bạn
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0). Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
Trước hết ta thấy O, A nằm trên cùng một mặt phẳng bờ \(\Delta\).
Qua A kẻ đường thẳng d vuông góc với \(\Delta\) tại H.
Đường thẳng d có phương trình: \(x+y-2=0\)
\(\Rightarrow H\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}x-y+2=0\\x+y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\Rightarrow H=\left(0;2\right)\)
Gọi A' là điểm đối xứng với A qua d
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=2x_H-x_A=-2\\y_{A'}=2y_H-y_A=4\end{matrix}\right.\Rightarrow A'=\left(-2;4\right)\)
\(\Rightarrow OA'=2\sqrt{5}\)
Phương trình đường thẳng OA': \(2x+y=0\)
Khi đó: \(OM+MA=OM+MA'\ge OA'=2\sqrt{5}\)
\(min=2\sqrt{5}\Leftrightarrow M\) là giao điểm của \(\Delta\) và OA'
\(\Leftrightarrow M\) có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}x-y+2=0\\2x+y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=\dfrac{4}{3}\end{matrix}\right.\Rightarrow M=\left(-\dfrac{2}{3};\dfrac{4}{3}\right)\)
Lời giải:
Vì $M$ thuộc $\Delta$ nên $M$ có tọa độ $(a-2,a)$
Độ dài đường gấp khúc $OMA$ là:
$OM+MA=\sqrt{a^2+(a-2)^2}+\sqrt{(a-4)^2+a^2}$
$=\sqrt{2}.(\sqrt{(a-1)^2+1}+\sqrt{(2-a)^2+2^2})$
$\geq \sqrt{2}.\sqrt{(a-1+2-a)^2+(1+2)^2}$ (theo BĐT Mincopxky)
$=2\sqrt{5}$
Vậy $OMA$ min bằng $2\sqrt{5}$. Giá trị này đạt tại $a=\frac{4}{3}$
Vậy $M(\frac{-2}{3},\frac{4}{3})$
Cho A, B là hai điểm biểu diễn hình học của hai số phức z 1 , z 2 z 1 ≠ 0 , z 2 ≠ 0 và thỏa mãn z 1 2 + z 2 2 = z 1 z 2 . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ).
A. Tam giác đều
B. Cân tại O
C. Vuông tại O
D. Vuông cân tại O.
Chọn đáp án A
Do z 2 ≠ 0 nên chia cả hai vế của z 1 2 + z 2 2 = z 1 z 2 cho z 2 2 , ta được:
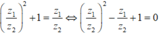
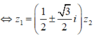
![]()
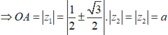
Ta có A B = z 1 - z 2 = a
Vậy OA = OB = AB hay tam giác OAB đều.
Trên đường thẳng xy lấy 23 điểm phân biệt và điểm O là điểm 0 nằm trên đường thẳng xy nối o với 23 điểm đó Hỏi có bao nhiêu góc đỉnh O mà cạnh đi qua hai trong 23 điểm thuộc đường thẳng xy đã cho
) Cho đường tròn ( O ; R ) có đường kính BD . Trên tiếp tuyến tại B của ( 0 ) lấy điểm M sao cho MB = BD = 2R . Gọi E là giao điểm của MD và ( 0 ) ( E + D ) . Từ M vẽ MA là tiếp tuyến của ( O ) ( A là tiếp điểm ) . Gọi H là giao điểm của OM và AB . a ) Chứng minh : Tứ giác MEHB nội tiếp và MA^2 = ME.MD b ) Tính MHE , c ) Gọi F là hình chiếu của A trên BD và K là giao điểm của AF và BE . Chứng minh A là trung điểm của FK
a) Vì BD là đường kính \(\Rightarrow\angle BED=90\)
Vì MB,MA là tiếp tuyến \(\Rightarrow\Delta MAB\) cân tại M và MO là phân giác \(\angle AMB\)
\(\Rightarrow MO\bot AB\Rightarrow\angle MHB=90\)
Ta có: \(\angle MHB=\angle MEB=90\Rightarrow MEHB\) nội tiếp
Xét \(\Delta MAE\) và \(\Delta MDA:\) Ta có: \(\left\{{}\begin{matrix}\angle MAE=\angle MDA\\\angle DMAchung\end{matrix}\right.\)
\(\Rightarrow\Delta MAE\sim\Delta MDA\left(g-g\right)\Rightarrow\dfrac{MA}{ME}=\dfrac{MD}{MA}\Rightarrow MA^2=MD.ME\)
b) MEHB nội tiếp \(\Rightarrow\angle MHE=\angle MBE=\angle MDB\)
Vì \(\Delta MBD\) vuông tại B có \(MB=BD=2R\Rightarrow\Delta MBD\) vuông cân tại B
\(\Rightarrow\angle MDB=45\Rightarrow\angle MHE=45\)
c) Xét \(\Delta MOB\) và \(\Delta BAF:\) Ta có: \(\left\{{}\begin{matrix}\angle MBO=\angle BFA=90\\\angle BOM=\angle BAF=\dfrac{1}{2}\angle BOA\end{matrix}\right.\)
\(\Rightarrow\Delta MOB\sim\Delta BAF\left(g-g\right)\Rightarrow\dfrac{AF}{AB}=\dfrac{OB}{MO}=\dfrac{OD}{MO}\left(1\right)\)
Vì \(\Delta MBD\) vuông cân tại B có \(BE\bot MD\Rightarrow\angle EBD=45\)
mà \(\Delta BFK\) vuông tại F \(\Rightarrow\Delta BFK\) vuông cân tại F \(\Rightarrow\angle BKF=45\)
Xét \(\Delta BAK\) và \(\Delta MOD:\) Ta có: \(\left\{{}\begin{matrix}\angle ABK=\angle DOM\left(MEHBnt\right)\\\angle BKA=\angle MDO=45\end{matrix}\right.\)
\(\Rightarrow\Delta MOD\sim\Delta BAK\left(g-g\right)\Rightarrow\dfrac{AK}{AB}=\dfrac{OD}{MO}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{AK}{AB}=\dfrac{AF}{AB}\Rightarrow AK=AF\Rightarrow\) đpcm

Trên trục số điểm 4 cách điểm 0 là 4 đơn vị theo chiều dương, điểm -4 cách điểm O là 4 đơn vị theo chiều âm. Điền vào chỗ trống trong các câu sau đây: a) Điểm -3 cách điểm O là ... đơn vị theo chiều .... b) Điểm 2 cách điểm O là ... đơn vị theo chiều ….
Cho hàm số f ( x ) = - 1 4 x có đồ thị (C) và các điểm M (0; 4); P (4; −1); Q (−4; 1); A (8; −2); O (0; 0). Có bao nhiêu điểm trong số các điểm trên thuộc đồ thị hàm số (C).
A. 4
B. 3
C. 2
D. 1
Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = - 1 4 x ta được:
+) Với M (0; 4), thay x = 0; y = 4 ta được 4 = - 1 4 .0 ⇔ 4 = 0 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = - 1 4 .0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (4; −1), thay x = 4 ; y = − 1 ta được −1 = - 1 4 . 4 ⇔ 1 = −1 (luôn đúng) nên P ∈ (C)
+) Với Q (−4; 1), thay x = − 4 ; y = 1 ta được 1 = - 1 4 .(−4) ⇔ 1 = 1 (luôn đúng) nên Q ∈ (C)
+) Với A (8; −2), thay x = 8 ; y = − 2 ta được −2 = - 1 4 .8 ⇔ −2 = −2 (luôn đúng) nên A ∈
Đáp án cần chọn là: A