Chọn C

Ta có:

u n + 1 − u n = − 3 ( n + 1 ) + 1 − ( − 3 n + 1 ) = − 3

 là hằng số

Suy ra dãy (u_n) là cấp số cộng với công sai d= -3.

Chọn D

Ta có:

u n + 1 − u n = 2 ( n + 1 ) + 3 − ( 2 n + 3 ) = 2

 là hằng số

Suy ra dãy (u_n) là cấp số cộng với công sai d= 2.

Đáp án A

Ta có:

u n + 1 − u n = n + 1 2 + 1 − ( n 2 + 1 ) = 2 n + 1

 phụ thuộc vào n.

 Suy ra dãy (u_n) không phải là cấp số cộng.

Chọn A

Ta có: u n + 1 u n = 4.3 n + 1 4.3 n = 3  không phụ thuộc vào n suy ra dãy ( u n )  là một cấp số nhân với công bội q = 3.

a) \({u_1} = 8;\;\;\;\;{u_2} = 13;\;\;\;\;\;{u_3} = 18;\;\;\;\;\;{u_4} = 23;\;\;\;\;\;{u_5} = 28\).

Ta có: \({u_n} - {u_{n - 1}} = 3 + 5n - \left[ {3 + 5\left( {n - 1} \right)} \right] = 5,\;\forall n \ge 2\).

Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 8\) và công sai \(d = 5\).

Số hạng tổng quát: \({u_n} = 8 + 5\left( {n - 1} \right)\).

b) \({u_1} = 2;\;\;\;\;{u_2} = 8;\;\;\;\;{u_3} = 14;\;\;\;\;\;{u_4} = 20;\;\;\;\;\;{u_5} = 26\).

Ta có: \({u_n} - {u_{n - 1}} = 6n - 4 - \left[ {6\left( {n - 1} \right) - 4} \right] = 6,\;\forall n \ge 2\).

Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2\) và công sai \(d = 6\).

Số hạng tổng quát: \({u_n} = 2 + 6\left( {n - 1} \right)\).

c) \({u_1} = 2;\;\;\;\;{u_2} = 4;\;\;\;\;\;{u_3} = 7;\;\;\;\;\;\;{u_4} = 11;\;\;\;\;\;\;\;{u_5} = 16\)

Ta có: \({u_n} - {u_{n - 1}} = n,\;\) n biến động.

Suy ra đây không phải là cấp số cộng.

d) \({u_1} = 2;\;\;\;\;{u_2} = 5;\;\;\;\;\;\;{u_3} = 8;\;\;\;\;\;\;{u_4} = 11;\;\;\;\;\;\;\;{u_5} = 14\)

Ta có: \({u_n} - {u_{n - 1}} = 3\).

Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2\) và công sai \(d = 3\).

Số hạng tổng quát: \({u_n} = 2 + 3\left( {n - 1} \right),\;\forall n \ge 2\).

Input: dãy A và N phần tử

Output: Là cấp số cộng hoặc không là cấp số cộng

Thuật toán:

- Bước 1: Nhập N và dãy A1,A2,...,An

- Bước 2: d←A2-A1; i←2;

-Bước 3: Nếu i>N thì in ra kết quả là cấp số cộng rồi kết thúc

- Bước 4: Nếu A_i+1-A_i khác d thì chuyền xuống bước 6

- Bước 5: i←i+1, quay lại bước 3

- Bước 6: Thông báo không phải là cấp số cộng rồi kết thúc

Cấp số cộng  u n  có công sai là d nên 

Ta có 

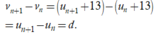
Vậy dãy số  v n  là một cấp số cộng có công sai cũng là d. Chọn C.

HD: D sai khi n = 1. Chọn D.