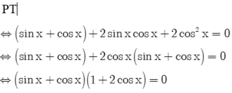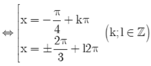Giải các phương trình sau cos2x - sinx - 1 = 0

Những câu hỏi liên quan
Giải các phương trình sau:
a, \(\dfrac{Sin^2x+Sinx}{Sinx-1}=-2\)
b,\(\dfrac{Cos2x+Sinx}{Sinx-1}+1=0\)
a)Đk:\(sinx\ne1\)
Pt\(\Leftrightarrow sin^2x+sinx=-2\left(sinx-1\right)\)
\(\Leftrightarrow sin^2x+3sinx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{-3+\sqrt{17}}{2}\left(tm\right)\\sinx=\dfrac{-3-\sqrt{17}}{2}\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\\x=\pi-arc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\end{matrix}\right.\)(\(k\in Z\))
b)Đk:\(sinx\ne1\)
Pt \(\Leftrightarrow\dfrac{1-2sin^2x+sinx}{sinx-1}+1=0\)
\(\Leftrightarrow\dfrac{-\left(sinx-1\right)\left(2sinx+1\right)}{sinx-1}+1=0\)
\(\Leftrightarrow-\left(2sinx+1\right)+1=0\)
\(\Leftrightarrow sinx=0\) (tm)
\(\Leftrightarrow x=k\pi,k\in Z\)
Vậy...
Đúng 1
Bình luận (0)
Giải phương trình lượng giác sau:
\(\dfrac{cos2x}{1-sinx}=0\)
Để giải phương trình cos(2x) - sin(x) = 0, ta có thể sử dụng các công thức lượng giác để đưa phương trình về dạng phù hợp.
Bước 1: Sử dụng công thức cos(2x) = 2cos^2(x) - 1, phương trình trở thành 2cos^2(x) - 1 - sin(x) = 0.
Bước 2: Sử dụng công thức sin^2(x) + cos^2(x) = 1, ta có thể thay thế cos^2(x) bằng 1 - sin^2(x), phương trình trở thành 2(1 - sin^2(x)) - 1 - sin(x) = 0.
Bước 3: Giải phương trình 2 - 2sin^2(x) - 1 - sin(x) = 0.
Bước 4: Đặt sin(x) = t, phương trình trở thành 2 - 2t^2 - 1 - t = 0.
Bước 5: Rút gọn phương trình, ta có -2t^2 - t + 1 = 0.
Bước 6: Giải phương trình bậc hai trên, ta có thể sử dụng công thức hoặc phân tích thành nhân tử để tìm giá trị của t.
Bước 7: Giải phương trình -2t^2 - t + 1 = 0, ta tìm được hai giá trị t = -1 và t = 1/2.
Bước 8: Đặt sin(x) = -1 và sin(x) = 1/2, ta tìm được hai giá trị x = -π/2 và x = π/6.
Vậy, phương trình cos(2x) - sin(x) = 0 có hai nghiệm là x = -π/2 và x = π/6.
Đúng 0
Bình luận (0)
ĐKXĐ: 1-sin x<>0
=>sin x<>1
=>x<>pi/2+k2pi
cos2x/1-sinx=0
=>cos2x=0
=>2x=pi/2+kpi
=>x=pi/2+kpi/2
Kết hợp ĐKXĐ, ta được: \(x\in\left\{pi+k2pi;\dfrac{3}{2}pi+k2pi;2pi+k2pi\right\}\)
Đúng 0
Bình luận (0)
giải phương trình: 3cosx(1 - cos2x) + 2sin2x + sinx + cos2x = 0
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
Đúng 0
Bình luận (0)
Giải phương trình: sinx + cosx + 1 + sin2x + cos2x = 0
![]()
![]()
![]()
![]()
giải phương trình sau:
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}\)=0
ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)
\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)
\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)
\(\Leftrightarrow2cos^22x-2cos2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)
Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
Câu 1: Tính tổng tất cả các nghiệm của phương trình sin3(x-dfrac{pi}{4}) sqrt{2}sinx trên đoạn [0 ; 2018]Câu 2: Tính tổng tất cả các nghiệm của phương trình cos2x (tan2x - cos2x) cos3x - cos2x + 1 trên đoạn [0 ; 43π]GIÚP MÌNH VỚI!!!
Đọc tiếp
Câu 1: Tính tổng tất cả các nghiệm của phương trình sin3(\(x-\dfrac{\pi}{4}\)) = \(\sqrt{2}\)sinx trên đoạn [0 ; 2018]
Câu 2: Tính tổng tất cả các nghiệm của phương trình cos2x (tan2x - cos2x) = cos3x - cos2x + 1 trên đoạn [0 ; 43π]
GIÚP MÌNH VỚI!!!![]()
Giải phương trình:
\(\sqrt{3}\left(Sinx-Cos2x\right)+Cosx+Sin2x=0\)
Cho phương trình:
4
cos
2
x
+
16
sin
x
cos
x
-
7
0
(
1
)
Xét các giá trị: Trong các giá trị trên, giá trị nào là nghiệm của phương trình (1)? A. Chỉ (III) B. (II) và (III) C. Chỉ (II) D. Chỉ (I)
Đọc tiếp
Cho phương trình: 4 cos 2 x + 16 sin x cos x - 7 = 0 ( 1 )
Xét các giá trị:
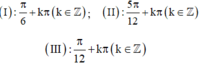
Trong các giá trị trên, giá trị nào là nghiệm của phương trình (1)?
A. Chỉ (III)
B. (II) và (III)
C. Chỉ (II)
D. Chỉ (I)
Đ á p á n B P T đ ã c h o t ư ơ n g đ ư ơ n g : 4 . cos 2 2 x + 8 sin 2 x - 7 = 0 ⇔ 4 . 1 - sin 2 2 x + 8 . sin 2 x - 7 = 0 ⇔ - 4 . sin 2 2 x + 8 . sin 2 x - 3 = 0 ⇔ sin 2 x = 1 2 ⇔ x = π 12 + k π ( k ∈ ℤ ) hoặc x = 5 π 12 + kπ ( k ∈ ℤ )
Đúng 0
Bình luận (0)
Giải phương trình
cos2x + cosx + 1= sin2x+sinx
\(cos2x+cosx+1=sin2x+sinx\)
\(\Leftrightarrow cos^2x-sin^2x+cosx+cos^2x+sin^2x=2sinx.cosx+sinx\)
\(\Leftrightarrow2cos^2x+cosx=2sinx.cosx+sinx\)
\(\Leftrightarrow cosx\left(2cosx+1\right)=sinx\left(2cosx+1\right)\)
\(\Leftrightarrow\left(2cosx+1\right)\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2cosx+1=0\\sinx=cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}cosx=-\dfrac{1}{2}\\tanx=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\x=\dfrac{\pi}{4}+k\pi\\\end{matrix}\right.\)
Đúng 0
Bình luận (0)