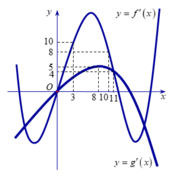
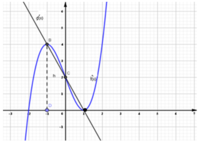
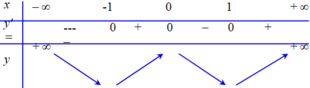
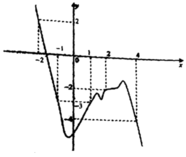
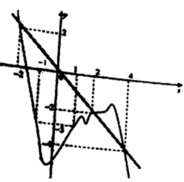
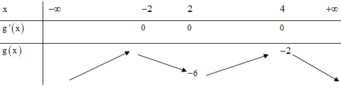
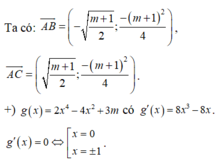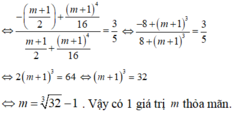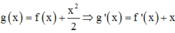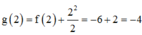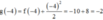Cho hai hàm số f ( x ) = x 2 và có g x = - x 2 + 2 n ế u x ≤ 1 2 n ế u - 1 < x < 1 - x 2 + 2 n ế u x ≥ 1 đồ thị như hình 55
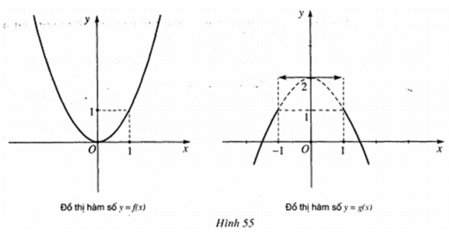
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1 ;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1 .