Tìm giá trị nhỏ nhất của hàm số: y = x 4 + 2 x 2 + 1 3 - 3 x 2 + 1 3 + 1
A. -1/2
B. -2/3
C. -5/4
D. Đáp án khác
Tìm giá trị nhỏ nhất của hàm số y = x - 2 + 4 - x trên đoạn [2;4].
A. m i n 2 ; 4 y = 3 2
B. m i n 2 ; 4 y = 3 2
C. m i n 2 ; 4 y = 2
D. m i n 2 ; 4 y = 2
Tìm giá trị nhỏ nhất của hàm số y = x - 2 + 4 - x trên đoạn [2;4].
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y=(3m-4)x\(^2\) với m\(\ne\)\(\dfrac{4}{3}\). Tìm các giá trị của tham số m để hàm số :
a) Đạt giá trị lớn nhất là 0
b) Đạt giá trị nhỏ nhất là 0
a) Để m đạt giá trị lớn nhất là 0 thì \(y=\left(3m-4\right)x^2\le0\) ⇔ \(3m-4\le0\)
⇔ \(m\le\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị lớn nhất là 0 thì \(m< \dfrac{4}{3}\)
b) Để m đạt giá trị nhỏ nhất là 0 thì \(y=\left(3m-4\right)x^2\ge0\) ⇔ \(3m-4\ge0\)
⇔ \(m\ge\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị nhỏ nhất là 0 thì \(m>\dfrac{4}{3}\)
Tìm giá trị nhỏ nhất của hàm số y = x(x +2)(x+4)(x+6) + 18.
Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x ∈ [−3; 4]
A. max − 3 ; 4 y = 4
B. min y = − 2 − 3 ; 4
C. Cả A, B đều đúng
D. Cả A, B đều sai
Tìm giá trị nhỏ nhất của hàm số y=x^2+2x-4 trên đoạn [-2;3]
A. – 4
B. – 12
C. 11
D. – 5
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
Lập bảng biến thiên của hàm số \(y = {x^2} + 2x + 3.\) Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
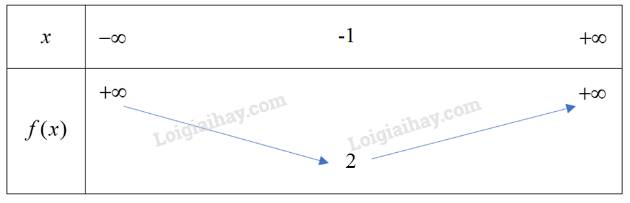
Hàm số đạt giá trị nhỏ nhất bằng \(2\).
Cho hàm số y=f(x)= -3x^2+10x-4 a) Lập bảng biến thiên và vẽ đồ thị hàm số y= f(×) b) Từ bảng biến thiên, xác định khoảng đồng biến và nghịch biến và giá trị nhỏ nhất của hàm số trên c) Từ bảng biến thiên tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn [-1;2]
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |

b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số trên đoạn [2;4]
y=\(\dfrac{x^2+3}{x-1}\)