Cho hàm số f ( x ) = sin 5 x 5 x x ≠ 0 a + 2 x = 0 . Tìm a để f(x) liên tục tại x = 0.
A. 1.
B. -1.
C. -2.
D. 2.
cho hàm số f(x)=\(\left(sin^23x-4\right)^5\) có đạo hàm là \(f'\left(x\right)=k\left(sin^23x-4\right)^4.sin3xcos3x\). hỏi k bằng bao nhiêu
Lời giải:
$f'(x)=5(\sin ^23x-4)'(\sin ^23x-4)^4=5.2.\sin 3x (\sin 3x)'.(\sin ^23x-4)^4$
$=30\sin 3x\cos 3x(\sin ^23x-4)^4$
$\Rightarrow k=30$
Cho hàm số \(y = f(u) = \sin u;\,\,u = g(x) = {x^2}\)
a) Bằng cách thay u bởi \({x^2}\) trong biểu thức \(\sin u\), hãy biểu thị giá trị của y theo biến số x.
b) Xác định hàm số \(y = f(g(x))\)
a: \(y=f\left(x^2\right)=sin\left(x^2\right)\)
b: \(y=f\left(g\left(x\right)\right)=f\left(x^2\right)=sinx^2\)
Cho hàm số y=f(x). Hàm số f'(x) có biến thiên
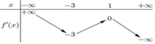
Bất phương trình f(sin x)< -3x + m đúng với mọi x ∈ - π 2 ; π 2 khi và chỉ khi
A. m ≥ f ( 1 ) + 3 π 2
B. m > f ( - 1 ) - 3 π 2
C. m > f ( π 2 ) + 3 π 2
D. m > f ( 1 ) + 3 π 2
Cho hàm số y = f(x) có bảng xét dấu biến thiên như sau:
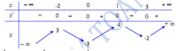
Giá trị lớn nhất của hàm số f(sin x - 1) bằng
A. 3
B. 3
C. -3
D. -2
Chọn B
Đặt ![]()
Bài toán quy về tìm giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0].
Từ bảng biến thiên ta có giá trị lớn nhất của hàm số y = f(t) trên đoạn [-2;0] là 3.
Vậy giá trị lớn nhất của hàm số f(sin x -1) bằng 3.
Tìm nguyên hàm F(x) của hàm số \(f\left(x\right)=\cos x+\sin x\) sao cho nguyên hàm đó thỏa mãn điều kiện F(0)=1
Một trong các nguyên hàm của hàm số \(f\left(x\right)=\cos x+\sin x\) là hàm số \(\sin x-\cos x\) . Từ định lí nếu hàm số f(x) có nguyên hàm F(x) trên khoảng (a,b) thì trên khoảng đó nó có vô số nguyên hàm và hai nguyên hàm bất kì của cùng một hàm cho trên khoảng (a,b) là sai khác nhau một hằng số cộng. suy ra mọi nguyên hàm số đã cho đều có dạng \(F\left(x\right)=\sin x-\cos x+C\), trong đó C là hằng số nào đó.
Để xác định hằng số C ta sử dụng điều kiện F(0)=1
Từ điều kiện này và biểu thức F(x) ta có :
\(\sin0-\cos0+C=1\Rightarrow C=1+\cos0=2\)
Do đó hàm số \(F\left(x\right)=\sin x-\cos x+2\) là nguyên hàm cần tìm
f(x)=4sin2x.cos2x.sinx=4(1-cos2x)cos2x.sinx=(4cos4x-4cos2x)(-sinx)
Đặt u=cosx ---> F(x)=(4/5)cos5x-(4/3)cos3x+C
Hàm số F(x) = ln|sin x – cos x| là một nguyên hàm của hàm số
A. f ( x ) = sin x + cos x sin x - cos x
B. f ( x ) = sin x - cos x sin x + cos x
C. f ( x ) = 1 sin x + cos x
D. f ( x ) = 1 sin x - cos x
Chọn A.
F ' ( x ) = sin x - cos x ' sin x - cos x = cos x + sin x sin x - cos x
Biết F(x) là một nguyên hàm của hàm số f(x) = sin x và đồ thị hàm số y = F(x) đi qua điểm M(0;1) . Tính F π 2 .
A. F π 2 = 0
B. F π 2 = 1
C. F π 2 = 2
D. F π 2 = - 1
Cho hàm số \(f\left( x \right) = 2x - \sin x,g\left( x \right) = \sqrt {x - 1} \).
Xét tính liên tục hàm số \(y = f\left( x \right).g\left( x \right)\) và \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\).
• Xét hàm số \(f\left( x \right) = 2x - \sin x\) có tập xác định \(D = \mathbb{R}\).
Vậy hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\).
• Xét hàm số \(g\left( x \right) = \sqrt {x - 1} \)
ĐKXĐ: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)
Hàm số \(g\left( x \right) = \sqrt {x - 1} \) có tập xác định \(D = \left[ {1; + \infty } \right)\).
Hàm số \(g\left( x \right) = \sqrt {x - 1} \) là hàm căn thức nên liên tục trên khoảng \(\left( {1; + \infty } \right)\).
Ta có: \(\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \sqrt {x - 1} = \sqrt {1 - 1} = 0 = g\left( 1 \right)\)
Do đó hàm số \(g\left( x \right) = \sqrt {x - 1} \) liên tục tại điểm \({x_0} = 1\).
Vậy hàm số \(g\left( x \right) = \sqrt {x - 1} \) liên tục trên nửa khoảng \(\left[ {1; + \infty } \right)\).
• Xét hàm số \(y = f\left( x \right).g\left( x \right) = \left( {2x - \sin x} \right)\sqrt {x - 1} \)
Do hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) đều liên tục tại mọi điểm \({x_0} \in \left[ {1; + \infty } \right)\) nên hàm số \(y = f\left( x \right).g\left( x \right)\) liên tục trên nửa khoảng \(\left[ {1; + \infty } \right)\).
• Xét hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{2x - \sin x}}{{\sqrt {x - 1} }}\)
Do hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) đều liên tục tại mọi điểm \({x_0} \in \left[ {1; + \infty } \right)\) nên hàm số \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục trên khoảng \(\left( {1; + \infty } \right)\).