chứng minh rằng (a+2)²+(a+4)²>0 với mọi số thực a

Những câu hỏi liên quan
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 =0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| < |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)
2 = 0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
a) chứng minh rằng a2 + ab + b2 >= 0 với mọi số thực a , b ; b) chứng minh rằng với 2 số thực a , b tùy ý , ta có a4 + b4 >= a3b + ab3
a)\(a^2+ab+b^2=a^2+\dfrac{2ab}{2}+\left(\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\)
\(=\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}\ge0\forall a,b\)
b)\(a^4+b^4\ge a^3b+ab^3\)
\(\Leftrightarrow a^3\left(a-b\right)-b^3\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a^3-b^3\right)\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\left(a^2+ab+b^2\right)\ge0\forall a,b\)
Đúng 0
Bình luận (0)
chứng minh rằng :
a)x2-x+1<0 với mọi số thực x
b)-x2+2x-4<0 với mọi số thực x
a) Đề sai thì phải.Phải là CM: \(x^2-x+1>0\) với mọi x
Ta có:
\(x^2-x+1=\left(x^2-x+\frac{1}{4}\right)+\frac{3}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\) nên \(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0\)
Vậy \(x^2-x+1>0\) với mọi \(x\in R\)
b)Ta có:
\(-x^2+2x-4=-\left(x^2-2x+1\right)-3\)
\(=-\left(x-1\right)^2-3\)
Vì \(-\left(x-1\right)^2\le0\) với mọi x nên \(-\left(x-1\right)^2-3< 0\)
Vậy \(-x^2+2x-4< 0\) với mọi \(x\in R\)
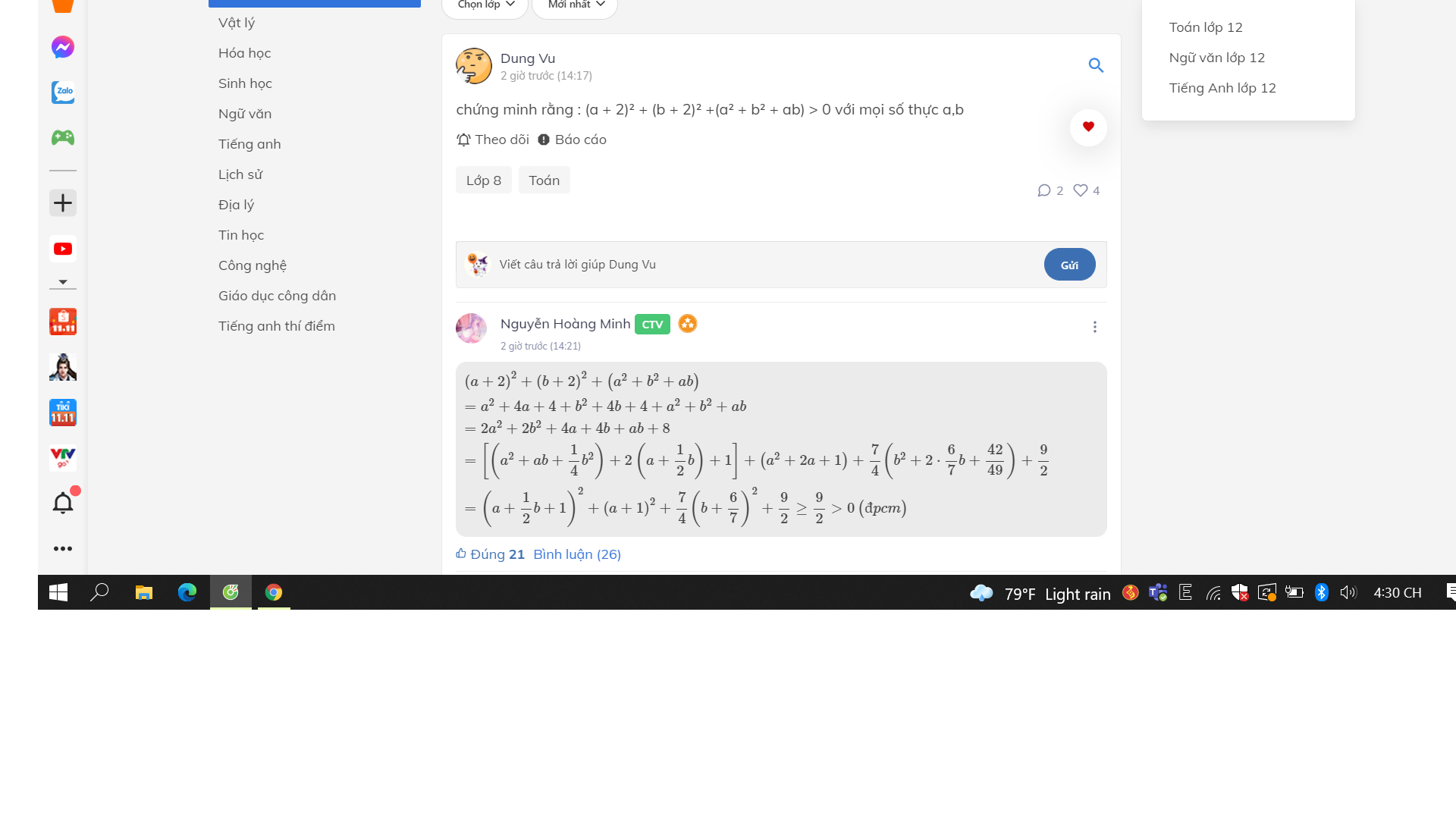
chứng minh rằng : (a + 2)² + (b + 2)² +(a² + b² + ab) > 0 với mọi số thực a,b
\(\left(a+2\right)^2+\left(b+2\right)^2+\left(a^2+b^2+ab\right)\\ =a^2+4a+4+b^2+4b+4+a^2+b^2+ab\\ =2a^2+2b^2+4a+4b+ab+8\\ =\left[\left(a^2+ab+\dfrac{1}{4}b^2\right)+2\left(a+\dfrac{1}{2}b\right)+1\right]+\left(a^2+2a+1\right)+\dfrac{7}{4}\left(b^2+2\cdot\dfrac{6}{7}b+\dfrac{42}{49}\right)+\dfrac{9}{2}\\ =\left(a+\dfrac{1}{2}b+1\right)^2+\left(a+1\right)^2+\dfrac{7}{4}\left(b+\dfrac{6}{7}\right)^2+\dfrac{9}{2}\ge\dfrac{9}{2}>0\left(đpcm\right)\)
Đúng 37
Bình luận (53)
Nó hot quá.2 giờ rồi câu hỏi đấy vẫn đứng ở đầu
Đúng 3
Bình luận (8)
Bài 6: Chứng minh rằng:
a)x2-x+1>0 với mọi số thực x
b)-x2+2x-4<0 với mọi số thực x
a) Ta có: \(x^2-x+1=x^2-2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Ta có: \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)
hay \(x^2-x+1>0\forall x\)(đpcm)
b) Ta có: \(-x^2+2x-4=-\left(x^2-2x+4\right)=-\left(x^2-2x+1+3\right)=-\left(x-1\right)^2-3\)
Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-1\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-1\right)^2-3\le-3< 0\forall x\)
hay \(-x^2+2x-4< 0\forall x\)(đpcm)
Bài 1.Tìm các số thực xthỏa mãn:a. |3 − |2x − 1| x − 1b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| 36c. |x − 2| + |x − 3| + ... + |x − 9| 1-x Bài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c 0. Chứng minh rằng: |a| + |b| + |c| là một số chẵn. Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c 2020. Tổng A |a − 1| + |b + 1| + |c − 2020|có thể bằng 2021 được không? Vì sao? Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn Bài 5. Tìm các số t...
Đọc tiếp
Bài 1.Tìm các số thực xthỏa mãn:a. |3 − |2x − 1| = x − 1b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| = 36c. |x − 2| + |x − 3| + ... + |x − 9| = 1-x
Bài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng: |a| + |b| + |c| là một số chẵn.
Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c = 2020. Tổng A = |a − 1| + |b + 1| + |c − 2020|có thể bằng 2021 được không? Vì sao?
Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2=0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 1.Tìm các số thực xthỏa mãn:a. |3 − |2x − 1| x − 1b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| 36c. |x − 2| + |x − 3| + ... + |x − 9| 1-x Bài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c 0. Chứng minh rằng: |a| + |b| + |c| là một số chẵn. Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c 2020. Tổng A |a − 1| + |b + 1| + |c − 2020|có thể bằng 2021 được không? Vì sao? Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn Bài 5. Tìm các số t...
Đọc tiếp
Bài 1.Tìm các số thực xthỏa mãn:a. |3 − |2x − 1| = x − 1b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| = 36c. |x − 2| + |x − 3| + ... + |x − 9| = 1-x
Bài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng: |a| + |b| + |c| là một số chẵn.
Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c = 2020. Tổng A = |a − 1| + |b + 1| + |c − 2020|có thể bằng 2021 được không? Vì sao?
Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2=0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 1.Tìm các số thực xthỏa mãn:a. |3 − |2x − 1| x − 1b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| 36c. |x − 2| + |x − 3| + ... + |x − 9| 1-x Bài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c 0. Chứng minh rằng: |a| + |b| + |c| là một số chẵn. Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c 2020. Tổng A |a − 1| + |b + 1| + |c − 2020|có thể bằng 2021 được không? Vì sao? Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn Bài 5. Tìm các số t...
Đọc tiếp
Bài 1.Tìm các số thực xthỏa mãn:a. |3 − |2x − 1| = x − 1b. |x − 1| + |2x − 2| + |4x − 4| + |5x − 5| = 36c. |x − 2| + |x − 3| + ... + |x − 9| = 1-x
Bài 2. Cho các số nguyên a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng: |a| + |b| + |c| là một số chẵn.
Bài 3. Cho các số nguyên a, b, c thỏa mãn a + b + c = 2020. Tổng A = |a − 1| + |b + 1| + |c − 2020|có thể bằng 2021 được không? Vì sao?
Bài 4. Cho các số nguyên a, b, c. Chứng minh rằng: |a − 2b| + |4b − 3c| + |c − 3a| là một số chẵn
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2=0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2











