Question

chứng minh rằng : (a + 2)² + (b + 2)² +(a² + b² + ab) > 0 với mọi số thực a,b

Answer 1

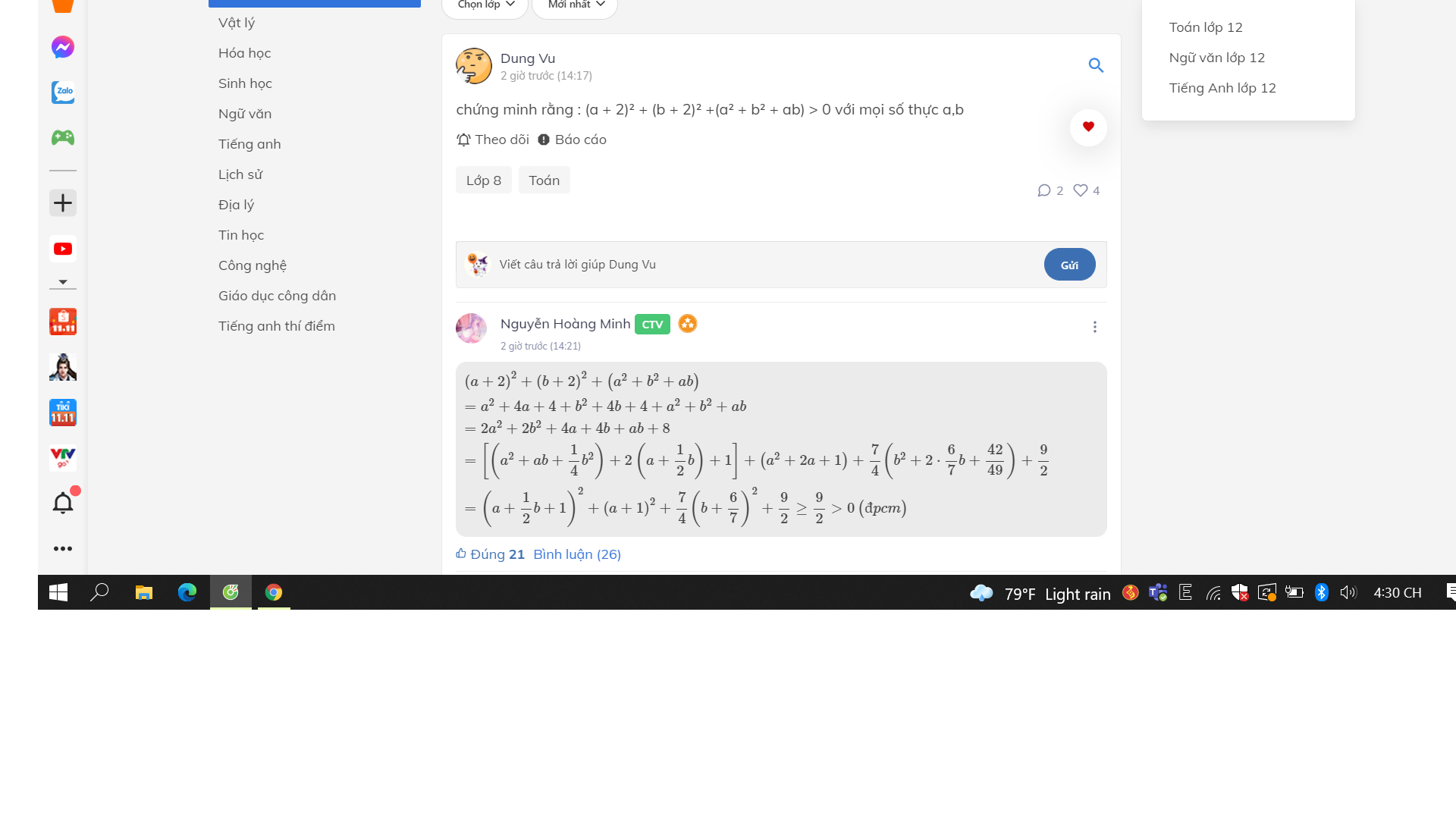
\(\left(a+2\right)^2+\left(b+2\right)^2+\left(a^2+b^2+ab\right)\\ =a^2+4a+4+b^2+4b+4+a^2+b^2+ab\\ =2a^2+2b^2+4a+4b+ab+8\\ =\left[\left(a^2+ab+\dfrac{1}{4}b^2\right)+2\left(a+\dfrac{1}{2}b\right)+1\right]+\left(a^2+2a+1\right)+\dfrac{7}{4}\left(b^2+2\cdot\dfrac{6}{7}b+\dfrac{42}{49}\right)+\dfrac{9}{2}\\ =\left(a+\dfrac{1}{2}b+1\right)^2+\left(a+1\right)^2+\dfrac{7}{4}\left(b+\dfrac{6}{7}\right)^2+\dfrac{9}{2}\ge\dfrac{9}{2}>0\left(đpcm\right)\)

Answer 2

Nó hot quá.2 giờ rồi câu hỏi đấy vẫn đứng ở đầu