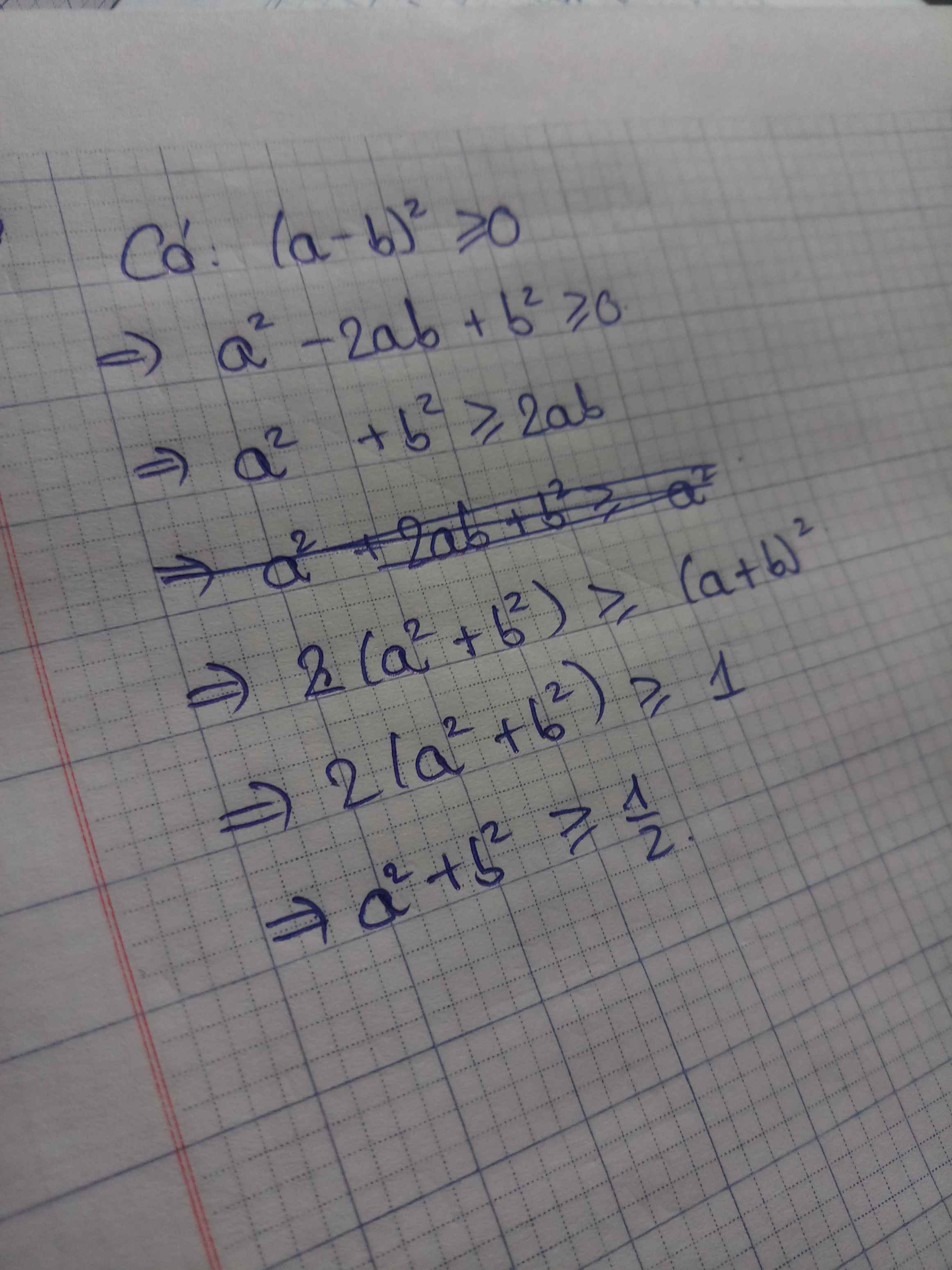Chứng minh rằng nếu a + b = 1 t h ì a 2 + b 2 ≥ 1 / 2

Những câu hỏi liên quan
a) So sánh các số a,b,c biết
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}\left(a,b,c\ne0\right)\)
b) Chứng minh rằng nếu\(a^2=bc\left(với a\ne b,a,c\ne0v\text{à a \ne}+-c\right)th\text{ì}\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)
a, Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=\dfrac{a+b+c}{b+c+a}=1\)
\(\Rightarrow a=b=c\)
b, Ta có: \(a^2=bc\Rightarrow\dfrac{a}{c}=\dfrac{b}{a}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{a}{c}=\dfrac{b}{a}=\dfrac{a+b}{c+a}=\dfrac{a-b}{c-a}\)
\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)
\(\Rightarrowđpcm\)
Đúng 0
Bình luận (0)
a) $\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=\dfrac{a+b+c}{b+c+a}=1$
(tính chất dãy tỉ số bằng nhau)
$\dfrac{a}{b}=1=>a=b$
$\dfrac{b}{c}=1=>b=c$
$\dfrac{c}{a}=1=>c=a$
Vậy a = b = c.
b) Ta có : $a^2=bc=>\dfrac{a}{c}=\dfrac{b}{a}=\dfrac{a+b}{c+a}=\dfrac{a-b}{c-a}$(tính chất dãy tỉ số bằng nhau)
$=>\dfrac{a+b}{c+a}=\dfrac{a-b}{c-a}$
$=>\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}$
Đúng 0
Bình luận (3)
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{a}=\dfrac{a+b+c}{b+c+a}=1\)
\(\Rightarrow\left\{{}\begin{matrix}a=b\\b=c\\c=a\end{matrix}\right.\)
\(\Rightarrow a=b=c\)
\(a^2=bc\Rightarrow\dfrac{a}{c}=\dfrac{b}{a}\)
Đặt:
\(\dfrac{a}{c}=\dfrac{b}{a}=k\)
\(\Rightarrow\left\{{}\begin{matrix}a=ck\\b=ak\end{matrix}\right.\)
\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{ck+ak}{ck-ak}=\dfrac{k\left(c+a\right)}{k\left(c-a\right)}=\dfrac{c+a}{c-a}\)
\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+a}{c-a}\)
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A;M là trung điểm của BC; Lấy E sao cho M là trung điểm của AE a: Chứng minh ABEC là hcn b: Lấy F sao cho B là trung điểm của AF .Gọi I là trung điểm của BE; Chứng minh rằng : IC=Ì
Tam giác ABC vuông tại A; M là trung điểm của BC ; Lấy E sao cho M là trung điểm của AE a: Chứng minh ABEC là hcn b: Lấy E sao cho B là trung điểm của AE . Gọi I là trung điểm của BE ; Chứng minh rằng IC=Ì
Sửa đề: Lấy F sao cho B là trung điểm của AF
a: Xét tứ giác ABEC có
M là trung điểm chung của AE và BC
nên ABEC là hình bình hành
Hình bình hành ABEC có \(\widehat{BAC}=90^0\)
nên ABEC là hình chữ nhật
b: ABEC là hình chữ nhật
=>AB//EC và AB=EC
AB=EC
BA=BF
Do đó: BF=EC
Xét tứ giác BFEC có
BF//EC
BF=EC
Do đó: BFEC là hình bình hành
=>BE cắt FC tại trung điểm của mỗi đường
mà I là trung điểm của BE
nên I là trung điểm của FC
=>IF=IC
Đúng 1
Bình luận (0)
a) So sánh các số a,b,c biết
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\left(a,b,c\ne0\right)\)
b) Chứng minh rằng nếu
\(a^2=bc\left(v\text{ới a\ne}b,a,c\ne0v\text{à a\ne}+-c\right)th\text{ì}\frac{a+b}{a-b}=\frac{c+a}{c-a}\)
Chỗ a/ne là dấu khác nha
theo tinh chat cua day ti so bang nhau ta co:
a/b=b/c=c/a =a+b+c/b+c+a=1
suy ra: a/b=1
b/c=1
c/a=1
vay a=b=c=
Đúng 0
Bình luận (0)
Chứng minh rằng nếu bán kính đường tròn nội tiếp của một tam giác bằng ì đường cao lớn nhất của tam giác đó không nhỏ hơn 1.
( giúp Được thì Giúp mình Nha! )
chứng minh rằng nếu a+b=1 thì a^2+b^2>=1/2
1)chứng minh rằng nếu a+b+c=1 thì a^4 +c^4 +b^4 =abc
2) với a,b,c dương chứng minh rằng 2căna +2cănb+2cănc +a^2+b^2+c^2 >= 3(a+b+c)
Cho a+b+c=1 và a^2+b^2+c^2=1
A. Nếu x/a=y/b=c/z. Chứng minh Rằng xy+yz+zx=0
B. Nếu a^3+b^3+c^3=1. Tính giá trị của a,b,c
A,
Ta có : a + b + c =1
<=> ( a +b + c) 2 = 1
<=> a2 + b2 + c2 + 2 (ab +bc +ac ) =1
=> ab + bc +ac = 0
Áp dụng tính chất của dãy tỉ số bằng nhau có :
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{z}=\dfrac{x+y+z}{a+b+c}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}x=a\left(x+y+z\right)\\y=b\left(x+y+z\right)\\z=c\left(x+y+z\right)\end{matrix}\right.\)
xy + yz +zx
= ab(x+y+z)2 + bc (x+y+z)2 + ca(x+y+z)2
= (ab+bc +ca ) ( x+y+z)2 =0
Đúng 0
Bình luận (0)
Cho ΔABCnhọn, đường cao BD, CE cắt nhau tại H
a) Chứng minh rằng AD.AC = AE.AB và ^ABC= ^ADE
b) Chứng minh rằng ΔHEDvà ΔHBCđồng dạng
c)Chứng minh rằng BE.BA CD.CA = BC²
d) Nếu ΔABCđều hãy tính tỉ số diện tíchΔHEDvà diện tích ΔABC
Bài 1. Cho 4 điểm A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC.
a/ Chứng minh rằng vectoMN 1/2(vectoAB + vecto CD).
b/. Gọi O là điểm trên đoạn MN thỏa OM2ON. Chứng minh rằng: vectoOA - 2vectoOB -2vectoOC +vectoOD vceto 0
Bài 2. Cho tam giác ABC có O, G, H lần lượt là tâm đường tròn ngoại tiếp, trọng tâm va trực tâm tam giác.
a/. Gọi D là điểm đối xứng của A qua O. Chứng minh rằng tứ giác BHCD là hình bình hành.
b/. Chứng minh rằng vectoHA + vectoHB + vectoHC 2vectoHO...
Đọc tiếp
Bài 1. Cho 4 điểm A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC.
a/ Chứng minh rằng vectoMN = 1/2(vectoAB + vecto CD).
b/. Gọi O là điểm trên đoạn MN thỏa OM=2ON. Chứng minh rằng: vectoOA - 2vectoOB -2vectoOC +vectoOD = vceto 0
Bài 2. Cho tam giác ABC có O, G, H lần lượt là tâm đường tròn ngoại tiếp, trọng tâm va trực tâm tam giác.
a/. Gọi D là điểm đối xứng của A qua O. Chứng minh rằng tứ giác BHCD là hình bình hành.
b/. Chứng minh rằng vectoHA + vectoHB + vectoHC = 2vectoHO
vectoOA + vectoOB + vectoOC = vectoOH
c/. Chứng minh rằng ba điểm O, G, H thẳng hàng
Ai biết giải giúp em với^^