Nêu cách giải phương trình trùng phương ax4 + bx2 + c = 0 (a ≠ 0)

Những câu hỏi liên quan
Nêu cách giải phương trình trùng phương a x 4 + b x 2 + c = 0 ( a ≠ 0 )
- Đặt ẩn phụ t = x 2 (1) (điều kiện t ≥ 0).
Khi đó phương trình đã cho tương đương với một phương trình bậc 2 ẩn t là:
a t 2 + b t + c = 0 ( 2 )
- Giải phương trình (2) để tìm t, so sánh với điều kiện.
- Thay giá trị t thỏa mãn vào (1) để tìm x.
Đúng 0
Bình luận (0)
Nêu cách giải phương trình trùng phương
ax4 + bx2 + c = 0 (a ≠ 0)
mình sẽ tick cho ai nhanh nhat
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Bạn tham khảo :
https://toancap2.net/chuyen-de-phuong-trinh-trung-phuong/
Chúc bạn học tốt
Hình vẽ dưới đây là đồ thị của hàm số trùng phương
y
f
x
a
x
4
+
b
x
2
+
c
,
a
≠
0
. Tìm tất cả các giá trị thực của tham số thực m để phương trình
f
x
log...
Đọc tiếp
Hình vẽ dưới đây là đồ thị của hàm số trùng phương y = f x = a x 4 + b x 2 + c , a ≠ 0 . Tìm tất cả các giá trị thực của tham số thực m để phương trình f x = log 3 m có 8 nghiệm phân biệt.
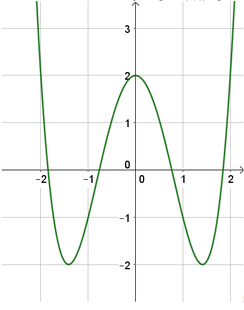
A. 1 < m < log 3 2 .
B. 1 < m < 9 .
C. m = 0 .
D. m > 1 .
Đáp án B
Ta có f x = f x v ớ i x ≥ 0 − f x v ớ i x < 0
Đồ thị hàm số y = f x được suy ra từ đồ thị hàm số y = f x gồm 2 phần:
- Phần 1: Phần phía bên trên trục hoành.
- Phần 2: Lấy đối xứng với phần phía dưới trục Ox qua trục Ox (bỏ đi phần phía dưới trục hoành).
Khi đó ta được đồ thị hàm số y = f x như sau:
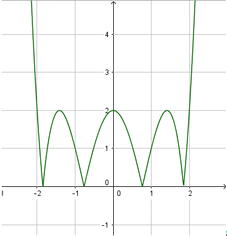
Phương trình f x = log 3 m có 8 nghiệm phân biệt ⇔ 0 < log 3 m < 2 ⇔ 1 < m < 9
Đúng 0
Bình luận (0)
tìm điều kiện để phương trình ax4+bx2+c=0 (a≠0) có 4 nghiệm phân biệt
Đặt x2=t \(\left(t\ge0\right)\)
=> pt 1 trở thành at2 + bt +c =0 \(\left(2\right)\)
Để pt 1 cso 4 nghiệm phân biệt thì pt 2 phải có 2 nghiệm dương phân biệt
=>\(\left\{{}\begin{matrix}a\ne0\\\Delta>0\\S>0\\P>0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Nếu phương trình ax4 + bx2 + c = 0 ( a khác 0) có hai nghiệm x1, x2 thì:
A. x1 + x2 = -b/a
B. x1 + x22 = -b/2a
C. x1 + x2 = 0
D. x1 . x2 = c/a
Cho phương trình
a
x
4
+
b
x
2
+
c
0
1
a
≠
0
. Đặt:
∆
b
2
-
4
a
c
,
S
-
b
a
,...
Đọc tiếp
Cho phương trình a x 4 + b x 2 + c = 0 1 a ≠ 0 . Đặt: ∆ = b 2 - 4 a c , S = - b a , P = c a Khi đó (1) có 4 nghiệm phân biệt khi và chỉ khi:
A. Δ > 0
B. Δ < 0 ∨ Δ ≥ 0 S < 0 P > 0
C. S > 0 P > 0
D. Δ > 0 S > 0 P > 0
Đặt t = x 2 t ≥ 0
Phương trình (1) thành a t 2 + b t + c = 0 2
Phương trình (1) có 4 nghiệm phân biệt
⇔ phương trình (2) có 2 nghiệm phân biệt dương ⇔ Δ > 0 S > 0 P > 0
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho phương trình
a
x
4
+
b
x
2
+
c
0
1
a
≠
0
. Đặt:
∆
b
2
-
4
a
c
,
S
-
b
a
,
...
Đọc tiếp
Cho phương trình a x 4 + b x 2 + c = 0 1 a ≠ 0 . Đặt: ∆ = b 2 - 4 a c , S = - b a , P = c a . Ta có (1) vô nghiệm khi và chỉ khi:
A. Δ < 0
B. Δ < 0 ∨ Δ ≥ 0 S < 0 P > 0
C. Δ > 0 S < 0
D. Δ > 0 P > 0
Đặt t = x 2 t ≥ 0
Phương trình (1) thành a t 2 + b t + c = 0 2
Phương trình (1) vô nghiệm
⇔ phương trình (2) vô nghiệm hoặc phương trình (2) có 2 nghiệm cùng âm
⇔ ∆ < 0 ⇔ Δ ≥ 0 S < 0 P > 0
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
(
a
,
b
,
c
∈
ℝ
)
có đồ thị như hình vẽ Số nghiệm thực của phương trình 2f(x) -3 0 bằng A. 0 B. 3 C. 2 D. 4
Đọc tiếp
Hàm số f ( x ) = a x 4 + b x 2 + c ( a , b , c ∈ ℝ ) có đồ thị như hình vẽ
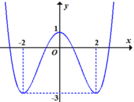
Số nghiệm thực của phương trình 2f(x) -3 =0 bằng
A. 0
B. 3
C. 2
D. 4
Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 38: Lấy một ví dụ về hàm số dạng y = ax4 + bx2 + c sao cho phương trình y’ = 0 chỉ có một nghiệm.
Ví dụ: Hàm số y = x4 + 2x2 có y' = 4x3 + 4x
Phương trình y' = 0 chỉ có một nghiệm x = 0
Đúng 1
Bình luận (1)
















