Cho Bx // Ny //Oz, O B x ^ = 130° và O N y ^ = 140°. Tính B O N ^
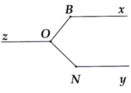
Cho Bx // Ny //Oz, O B x ^ = 130 ° v à O N y ^ = 140 ° . Tính B O N ^ .
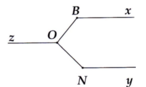
Cho Bx // Ny // Oz ; góc OBx= 130 độ, góc ONy= 140 độ. Tính góc BON
Do Bx // Oz => góc BOz' = góc xBO = 180o (Do 2 góc trong cùng phía)
mà góc xBO = 130o
=> góc BOz' + 130o = 180o
=> góc BOz' = 180o - 130o= 50o
Do Oz // Ny mà Oz' là tia đối của tia Oz => Oz' // Ny
=> z'ON + ONy = 180o ( do 2 góc trong cùng phía)
mà góc ONy = 140o
=> z'ON + 140o = 180o
=> z'ON = 180o - 140o = 40o
Ta thấy: góc BON = góc BOz' + z'ON = 50o + 40o = 90o
Vậy góc BON= 90o
cho Bx // Ny // Oz, OBx=130 độ và ONy=140 độ.vẽ hình
Bài 1: Cho hai tia Oy và Oz cùng nằm trên nửa mặt phẳng có bờ chứa tia Ox sao cho xÔy = 60o, xÔz = 130o
a, trong ba tia Oy, Oz, Ox tia nào nằm giữa 2 tia còn lại? vì sao?
b, so sánh xÔy và yÔz
c, vẽ tia Ox' là tia đối của tia Ox . tính góc x'Oz
a/vì \(60^o< 130^o\)hay \(\widehat{xOy}< \widehat{xOz}\)
nên Oy nằm giữa 2 tia Ox à Oz
b/ta có: góc xOy+góc yOz=xOz
=>góc yOz=góc xOz-góc xOy=130o-60o=70o
vì 70o>60onên góc yOz>góc xOy
c/ta có Ox' là tia đối của Ox
=> góc xOx'=180o
=>góc xOz+góc zOx'=180o
=> góc zOx'=60o
Cho góc bẹt \(x\widehat{Oy}\). Gọi Ot và Oz là hai tia cùng nằm trên một nửa mặt phẳng có bờ Ox sao cho \(x\widehat{Ot=130^o}\)và \(y\widehat{Oz=100^o}\)
a) Tính số đo góc \(z\widehat{Ot}\)
b) Vì sao Ot là tia phân giác của góc \(y\widehat{Oz?}\)
Có góc xOt + góc yOt=180' (2 gocke bu)
130' + góc yOt =180'
goc yOt=180'-130'
gocyOt=50'
Có góc yOt+góc tOz=góc yOz(Ot nằm giữa Oz và Oy)
50'+goctOz=100'
góc tOz=100'-50'
góc tOz=50'
b,co gocyOt=goc tOz=50'
suy ra Ot là phân giác của xOy
cho Bx // Ny // Oz, \(\widehat{OBx}\)=130\(^0\)và \(\widehat{ONy}\)=140\(^0\). tính \(\widehat{BON}\)
Ta có: ^OBx + ^BOz = 1800 ( trong cùng phía của Bx // Oz)
=> ^BOz = 1800 - ^BOx = 1800 - 1300 = 500
^zON + ^ONy = 1800 (trong cùng phía của Oz // Ny)
=> ^zOn = 1800 - ^ONy = 1800 - 1400 = 400
Vậy: ^BON = ^BOz + ^zOn = 500 + 400 = 900
Lấy điểm O bất kì trên đường thẳng xy. Trên nửa mặt phẳng bờ xy, vẽ tia Oz sao cho xOz = 50o. Trên tia Oy, lấy điểm B. Trên nửa mặt phẳng bờ xy chứa Oz, vẽ Bt sao cho tBy =130o.
a) chứng minh Oz // Bt
b) vẽ Om và Bn sao cho lần lượt là các tia phân giác của xOz và xBt. Chứng minh Om // Bt
a, Ta có: tBy + tBO = 180o (2 góc kề bù)
=> 130o +tBO = 180o
=> tBO = 50o
=> tBO = xOz = 50o
Mà 2 góc này nằm ở vị trí đồng vị
=> Oz // Bt (dhnb)
b, Vì Om là phân giác xOz
=> xOm = mOz = xOz/2 = 50o/2 = 25o
Vì Bn là phân giác xBt
=> xBn = nBt = xBt/2 = 50o/2 = 25o
=> xOm = xBn = 25o
Mà 2 góc này nằm ở vị trí đồng vị
=> Om // Bn (dhnb)
Lấy điểm O bất kì trên đường thẳng xy. Trên nửa mặt phẳng bờ xy, vẽ tia Oz sao cho xOz = 50o. Trên tia Oy, lấy điểm B. Trên nửa mặt phẳng bờ xy chứa Oz, vẽ Bt sao cho tBy =130o.
a) chứng minh Oz // Bt
b) vẽ Om và Bn sao cho lần lượt là các tia phân giác của xOz và xBt. Chứng minh Om // Bt
làm xong trước tích cho
a) Ta có: \(\widehat{tBy}+\widehat{tBO}=180^0\) (vì 2 góc kề bù)
=> \(130^0+\widehat{tBO}=180^0\)
=> \(\widehat{tBO}=180^0-130^0\)
=> \(\widehat{tBO}=50^0.\)
Mà \(\widehat{xOz}=50^0\left(gt\right)\)
=> \(\widehat{tBO}=\widehat{xOz}=50^0\)
Mà 2 góc này nằm ở vị trí đồng vị.
=> \(Oz\) // \(Bt.\)
b) Vì \(Om\) là tia phân giác của \(\widehat{xOz}\left(gt\right)\)
=> \(\widehat{xOm}=\widehat{mOz}=\frac{\widehat{xOz}}{2}=\frac{50^0}{2}=25^0\) (1)
Vì \(Bn\) là tia phân giác của \(\widehat{xBt}\left(gt\right)\)
=> \(\widehat{xBn}=\widehat{nBt}=\frac{\widehat{xBt}}{2}=\frac{50^0}{2}=25^0\) (2)
Từ (1) và (2) => \(\widehat{xOm}=\widehat{xBn}=25^0\)
Mà 2 góc này nằm ở vị trí đồng vị.
=> \(Om\) // \(Bn\left(đpcm\right).\)
Chúc bạn học tốt!
Bài 6: Cho 2 tia Oy và Oz cùng nằm trên nửa mặt phẳng bờ Oi. Biết góc xOy = 50o, góc xOz = 130o.
a, Trong ba tia Ox, Oy, Oz, tia nào nằm giữa hai tia còn lại?
b, Tính góc yOz.
c, Vẽ tia Oz' là tia đối của tia Oz. Chứng minh rằng: Oi là phân giác của góc yOz'.
a, Vì \(\widehat{iOz}>\widehat{iOy}\left(130^o>50^o\right)\)nên tia Oy nằm giưa 2 tia còn lại
b, Vì tia Oy nằm giữa nên ta có:
\(\widehat{iOy}+\widehat{yOz}=\widehat{iOz}\)
\(50^o+\widehat{yOz}=130^o\)
\(\widehat{yOz}=130^o-50^o\)
\(\widehat{yOz}=80^o\)
c, Ta có: \(\widehat{iOz}+\widehat{iOz'}=180^o\) (kề bù)
\(130^o+\widehat{iOz'}=180^o\)
\(\widehat{iOz'}=180^o-130^o\)
\(\widehat{iOz'}=50^o\)
\(\Rightarrow\widehat{iOy}=\widehat{iOz'}\)
\(\Rightarrow\widehat{yOz'}=50^o+50^o=100^o\)
Vì \(\widehat{iOy}=\widehat{iOz'}=\dfrac{\widehat{yOz'}}{2}=\dfrac{100^o}{2}=50^o\)
nên tia Oi là tia phân giác của \(\widehat{yOz'}\)