Tập xác định của hàm số f(x)và g(x) đều là ℝ .

Với  x ∈ ℝ  thì  - x ∈ ℝ  và ta có: f - x = - - x = - x = f x ;

g - x = - x + 1 - - x - 1 = x - 1 - x + 1 = - g x .

Vậy f(x)là hàm số chẵn, g(x) là hàm số lẻ. Đáp án là D.

\(TXD\) \(D=R\backslash\left\{0\right\}\) là tập đối xứng.

\(\forall x\in D\Rightarrow-x\in D\)

Có \(f\left(-x\right)=\dfrac{\left(-x\right)^2+1}{\left|2\left(-x\right)+1\right|+\left|2\left(-x\right)-1\right|}\)

\(=\dfrac{x^2+1}{\left|1-2x\right|+\left|-2x-1\right|}\)

\(=\dfrac{x^2+1}{\left|-\left(2x-1\right)\right|+\left|-\left(2x+1\right)\right|}\)

\(=\dfrac{x^2+1}{\left|2x-1\right|+\left|2x+1\right|}\) \(=f\left(x\right)\)

Vậy hàm số \(y=f\left(x\right)=\dfrac{x^2+1}{\left|2x+1\right|+\left|2x-1\right|}\) là hàm số chẵn.

TXĐ: D=R

Khi \(x\in D\) thì \(-x\in D\)

\(f\left(-x\right)=\dfrac{\left(-x\right)^2+1}{\left|-2x+1\right|+\left|-2x-1\right|}\)

\(=\dfrac{x^2+1}{\left|2x+1\right|+\left|2x-1\right|}=f\left(x\right)\)

=>f(x) chẵn

Đáp án A

Đáp án B

+ Hàm số f(x)  và g(x)  đều có tập xác định là D= R.

+ Xét hàm số y=f(x)  : Với mọi  và

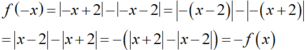
Nên y= f(x)  là hàm số lẻ.

+ Xét hàm số  y = g(x) :

 Với mọi  nên y = g(x)  là hàm số chẵn.

Chọn B.

Đáp án B

TXĐ: D=[-4;4]

\(f\left(-x\right)=\sqrt{4-\left(-x\right)}+\sqrt{-x+4}\)

\(=\sqrt{4-x}+\sqrt{4+x}\)

=f(x)

=>f(x) là hàm số chẵn