Giải phương trình tan( π 3 - x).tan( π 3 + 2x) = 1
A. x = π 6 + kπ
B. x = - π 3 + kπ
C. x = - π 6 + kπ
D. Vô nghiệm
Mấy bạnn giải chii tiết raa giúp mik với nhaa Câu 1: nghiệm dương nhỏ nhất của pt tan x=tan (6π/5) A. x=π/5 B. x=6π/5 C. x=6/5 D. x=6π Câu 2: tìm nghiệm thuộc đoạn [0;π] của pt cot 2x=cot(π/2-x) A. 2 B. 3 C.1 D.4 Câu 3: tìm tổng các nghiệm thuộc khoảng (-π/2;π/2) của pt 4sin²2x-1=0 A.0 B. π/6 C. π/3 D. π Câu 4: tìm tổng các nghiệm của pt cos(x+π/4)=1/2 trong khoảng (-π;π) A. π/2 B. -π/2 C. -3π/2 D. π/4
Giải phương trình sau: tanx + tan (x+π/4) = 1
Điều kiện:
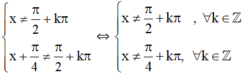
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
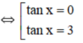
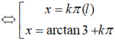
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
Đặt u = π/2 - x thì u' = -1
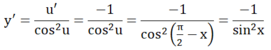
Do cos(π/2-x) = sinx
Giải phương trình: Tan(x-π/4) = Tan2x
\(\Leftrightarrow2x=x-\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\) (\(k\in Z\))
Phương trình tan ( x + π/ 3) có nghiệm là:
![]()
![]()
![]()
![]()
Giải pt: \( \tan ( 2x- \frac{ \pi }{ 3 } ) =- \frac{ 1 }{ 2 } \) với 0<x<π
ĐK: \(x\ne\dfrac{5\pi}{12}+\dfrac{k\pi}{2}\)
\(tan\left(2x-\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow2x-\dfrac{\pi}{3}=arctan\left(-\dfrac{1}{2}\right)+k\pi\)
\(\Leftrightarrow2x=\dfrac{\pi}{3}+arctan\left(-\dfrac{1}{2}\right)+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{1}{2}arctan\left(-\dfrac{1}{2}\right)+\dfrac{k\pi}{2}\in\left(0;\pi\right)\)
...
Phương trình 2 sin 2 2 x − 5 sin 2 x + 2 = 0 có hai họ nghiệm dạng x = α + kπ , x = β + kπ 0 < α , β < π . Khi đó tích αβ là
A. 5 π 2 36
B. 5 π 2 144
C. - 5 π 2 36
D. - 5 π 2 144
Số nghiệm thuộc khoảng ( 0 ; π ) của phương trình. tan x + sin x + tan x - sin x = 3 tan x là
A. 0
B. 1
C. 2
D. 3
Sin(x-π/2)+cos(x-π)+tan(5π/2-x)+tan(x-π/2)=-2cosx
\(sin\left(x-\dfrac{\pi}{2}\right)+cos\left(x-\pi\right)+tan\left(\dfrac{5\pi}{2}-x\right)+tan\left(x-\dfrac{\pi}{2}\right)\)
\(=-sin\left(\dfrac{\pi}{2}-x\right)+cos\left(\pi-x\right)+tan\left(2\pi+\dfrac{\pi}{2}-x\right)-tan\left(\dfrac{\pi}{2}-x\right)\)
\(=-cosx-cosx+tan\left(\dfrac{\pi}{2}-x\right)-cotx\)
\(=-2cosx+cotx-cotx=-2cosx\)
Phương trình tan( x - π/4) = 0 có nghiệm là:
A. x = π/4 + kπ, k ∈ Z.
B. x = 3π/4 + kπ, k ∈ Z.
C. x = kπ, k ∈ Z.
D. x = k2π, k ∈ Z.