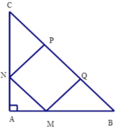
Cho hình vuông MNPQ nội tiếp tam giác ABC vuông cân tại A (hình vẽ). Biết S M N P Q = 484 c m 2 . Tính S A B C
A. 1089 c m 2
B. 1809 c m 2
C. 1089 2 c m 2
D. 2178 c m 2
Cho hình vuông MNPQ nội tiếp tam giác ABC vuông cân tại A. Biết Smnpq=484cm2. Tính Sabc.
Cho tam giác đều ABC cạnh 1 và hình vuông MNPQ nội tiếp trong tam giác ABC(M ∈ AB, N ∈ AC, P,Q ∈ BC) . Gọi S là phần mặt phẳng chứa các điểm thuộc tam giác ABC nhưng không chứa các điểm thuộc hình vuông MNPQ. Thể tích của vật thể tròn xoay khi quay S quanh trục là đường thẳng qua A vuông góc với BC là:
A . 810 - 467 3 24 π
B . 4 3 - 3 96 π
C . 4 3 - 3 96
D . 54 - 31 3 12 π
Đáp án A
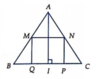
Gọi cạnh hình vuông là x. Ta có ![]()
![]()
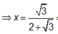
![]()
Gọi V 1 là thể tích hình nón khi quay tam giác ABC quanh trục trung tuyến AI , V 2 là thể tích hình trụ khi quay hình vuông MNPQ quanh trục AI thì
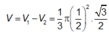
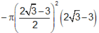
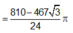
Cho tam giác ABC vuông cân tại A có BC = 36 cm. Vẽ hình chữ nhật MNPQ sao cho M thuộc AB ; N , P thuộc BC ; Q thuộc AC
tính diện tích lớn nhất của hình chữ nhật MNPQ
Trl :
-Câu này có trong Vio Toán tv lớp 8 ( tớ vừa mới thi ạ :33 )
-Hơi ngại làm :> Nhưng cho cậu kq nhé : 162 cm2
100%
Cho tam giác ABC vuông cân tại A. BC = 36cm. Vẽ hình chữ nhật MNPQ có M thuộc AB; Q thuộc AC; P,N thuộc BC . Xác định vị trí của MN để diện tích MNPQ lớn nhất
Cho tam giác ABC vuông cân tại A. BC = 36cm. Vẽ hình chữ nhật MNPQ có M thuộc AB; Q thuộc AC; P,N thuộc BC . Xác định vị trí của MN để diện tích MNPQ lớn nhất
xét tam giác ABC có các góc B,C nhọn trên nửa mặt phẳng bờ BC không chứa điểm A người ta dựng hình vuông BCDE.Nối AE và AD theo thứ tự cắt BC tại M và N Qua M và N kẻ các đường thẳng vuông góc với BC tương ứng cắt AB và AC tại P và Q
a) Chứng minh PQ song song BC
b)Chứng minh MNPQ là hình vuông
c) Giả sử tam giác ABC cân tại A có BC=10cm, tg góc B =2/3 Tình cạnh hình vuông nội tiếp
Cho ▲ABC vuông cân tại A. Trên BC lấy M,N sao cho BM=CN< . MQ vuông góc BC, NP vuông góc BC ( Q ϵ AB, P ϵ AC).
a) Tứ giác MNPQ là hình gì?
b) Xác định vị trí của M và N để MNPQ là hình vuông.
a: \(NP\perp BC;MQ\perp BC\)
Do đó: NP//MQ
ΔMQB vuông tại M có \(\widehat{B}=45^0\)
nên ΔMQB vuông cân tại M
=>MQ=MB
ΔNPC vuông tại N có \(\widehat{C}=45^0\)
nên ΔNPC vuông cân tại N
=>NP=NC
NP=NC
MQ=MB
NC=MB
Do đó: NP=MQ
Xét tứ giác MNPQ có
NP//MQ
NP=MQ
Do đó: MNPQ là hình bình hành
mà \(\widehat{PNM}=90^0\)
nên MNPQ là hình chữ nhật
b: Để MNPQ là hình vuông thì QM=MN
=>MB=MN
=>\(MB=MN=NC\)
=>\(MN=\dfrac{BC}{3}\)
Vậy: M,N nằm trên đoạn BC sao cho \(CN=NM=MB=\dfrac{CB}{3}\) thì MNPQ là hình vuông
Cho hình chóp S.ABC có tam giác ABC vuông tại A, tam giác SAC vuông cân tại S. Biết AB=a, AC=2a, S A C ⊥ A B C . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
A. 2 πa 2
B. 4 πa 2
C. 5 πa 2
D. 3 πa 2
Cho hình chóp S.ABC có tam giác ABC vuông tại A, tam giác SAC vuông cân tại S. Biết AB = a, Ac = 2a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
A. 2 π a 2
B. 4 π a 2
C. 5 π a 2
D. 3 π a 2
Chọn C.
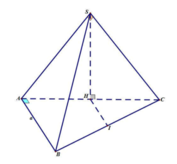
Gọi H, I lần lượt là trung điểm của BC, AC.
Tam giác SAC vuông cân tại S
Tam giác ABC vuông tại A => IA= IB = IC (1).
Lại có:
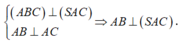
Mà HI là đường trung bình của tam giác ABC
![]()
![]()
![]()
Do đó: I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
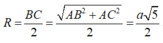
Vậy diện tích mặt cầu là
![]()