Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB’D’.
A. 3
![]()
C. 2
![]()
Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB’D’.
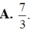
![]()
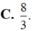
![]()
Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB’D’.
A. 7 3
B. 3
C. 8 3
D. 2
Đáp án B.
Ta có V A C B ' D ' = V A B C D . A ' B ' C ' D ' - V D ' . A C D - V C . A ' B ' D ' - V B ' . A B C
= V A B C D . A ' B ' C ' D ' - 4 . 1 6 V A B C D . A ' B ' C ' D ' = 1 3 V V A B C D . A ' B ' C ' D ' .
Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số giữa thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
Cho hình hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’
A. 7 3
B. 3
C. 8 3
D. 2
Cho hình hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
A. 7 3
B.3
C. 8 3
D.2
Đáp án B
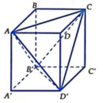
Nhìn hình vẽ ta thấy sẽ khó tính trực tiếp thể tích của khối tứ diện A C B ' D ' , do vậy ta sẽ tính gián tiếp.
Ta tính thể tích các khối tứ diện A C D D ' ; A A ' D ' B ' ; A B C B ' ; C C ; B ' D ' . Sau đó lấy thể tích khối hộp trừ đi tổng thể tích các khối trên.
Ta nhận thấy cả bốn khối tự diện A C D D ' ; A A ' D ' B ' ; A B C B ' ; C C ; B ' D ' đều có thể tích bằng nhau và bằng V 1 = 1 3 A A ' . 1 2 S A B C D = 1 6 V A B C D . A ' B ' C ' D ' = 1 6 V
Thể tích của khối tứ diện A C B ' D ' bằng V 2 = V − 4 6 V = V 3
Tỉ số cần tìm là 3. Ta chọn B
Cho hình hộp ABCD. A’B’C’D’. Tính tỉ số thể tích của khối tứ diện BDA’C’ và khối hộp ABCD.A’B’C’D’.
A. 1/5
B. 2/3
C. 1/3
D. 2/5
Cho khối hộp ABCD.A’B’C’D’. Gọi E và F theo thứ tự là trung điểm của các cạnh BB’ và DD’. Mặt phẳng (CEF) chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó.
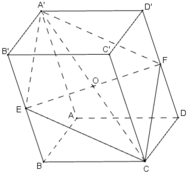
Gọi O là tâm hình hộp và tâm của hình bình hành BB’D’D. Khi đó O là trung điểm của EF.
Ta có: A’ ∈ CO (1)
CO ⊂ mp(CEF)(2)
Mặt khác A’E // CF, A’F // CE
Nên mp(CEF) cắt hình hộp theo thiết diện là hình bình hành A’ECF.
mp(CEF) chia hình hộp ABCD.A’B’C’D’ thành hai khối đa diện (Đ) và (Đ’).
Gọi (Đ) là khối đa diện có các đỉnh là A, B, C, D, A’, E, F và (Đ’) là khối đa diện còn lại.
Phép đối xứng qua tâm O biến các đỉnh A, B, C, D, A’, E, F của đa diện (Đ) lần lượt thành các đỉnh C’, D’, A’, B’, C, F, E của khối da diện (Đ’)
Suy ra phép đối xứng qua tâm O biến (Đ) thành (Đ’), nghĩa là hai hình đa diện (Đ) và (Đ’) bằng nhau.
Vậy tỉ số thể tích của (Đ) và (Đ’) bằng 1.
Cho khối hộp A B C D . A ' B ' C ' D ' . Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB'D'
A. 7 3
B. 3
C. 8 3
D. 2
Khối lăng trụ đều ABCD.A’B’C’D’ có thể tích 24 c m 3 . Tính thể tích V của khối tứ diện ACB’D’.
A. V = 8 c m 3
B. V = 6 c m 3
C. V = 12 c m 3
D. V = 4 c m 3
Đáp án A
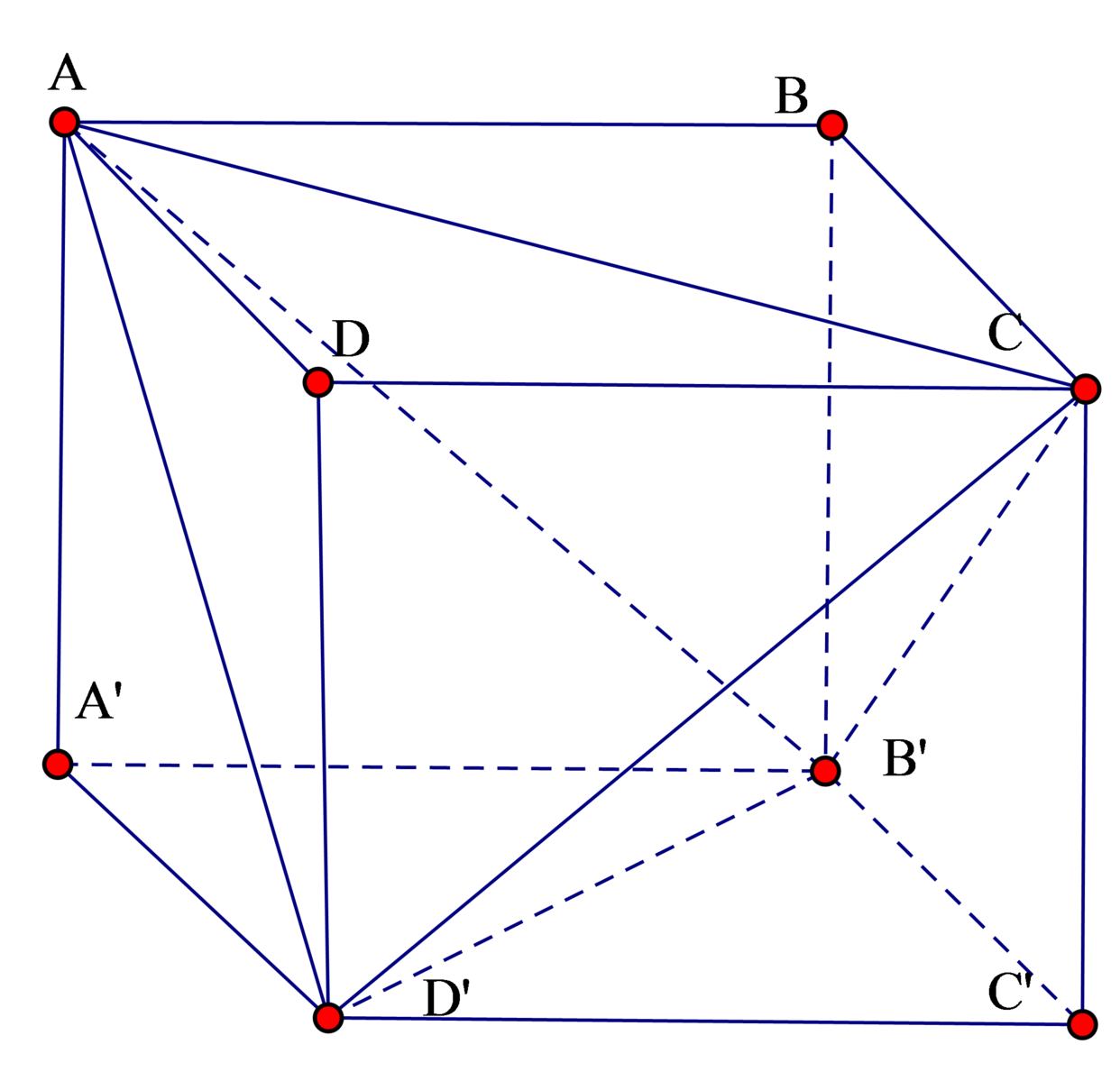
Gọi độ dài cạnh đáy là a, độ dài cạnh bên là b ta có:
V A B C D . A ' B ' C ' D ' = a 2 b = 24 c m 3
Tứ diện ACB'D' có các cặp đối bằng nhau
A C = B ' D ' = 2 a , A B ' = C D ' = A D ' = C B ' = a 2 + b 2
Áp dung công thức tính thể tích của tứ diện có các cặp đối bằng nhau ta có:
V A C B ' D ' = 1 6 2 2 a 2 2 b 2 2 a 2 = 1 3 a 2 b = 1 3 .24 = 8 c m 3
(Do tính đối xứng ta có thể tính:
V A C B ' D ' = V A B C D . A ' B ' C ' D ' − 4 V A . A ' B ' D ' = 24 − 4. 1 6 .24 = 8 c m 3 )