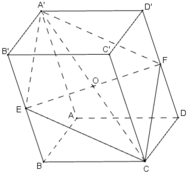
Gọi O là tâm hình hộp và tâm của hình bình hành BB’D’D. Khi đó O là trung điểm của EF.
Ta có: A’ ∈ CO (1)
CO ⊂ mp(CEF)(2)
Mặt khác A’E // CF, A’F // CE
Nên mp(CEF) cắt hình hộp theo thiết diện là hình bình hành A’ECF.
mp(CEF) chia hình hộp ABCD.A’B’C’D’ thành hai khối đa diện (Đ) và (Đ’).
Gọi (Đ) là khối đa diện có các đỉnh là A, B, C, D, A’, E, F và (Đ’) là khối đa diện còn lại.
Phép đối xứng qua tâm O biến các đỉnh A, B, C, D, A’, E, F của đa diện (Đ) lần lượt thành các đỉnh C’, D’, A’, B’, C, F, E của khối da diện (Đ’)
Suy ra phép đối xứng qua tâm O biến (Đ) thành (Đ’), nghĩa là hai hình đa diện (Đ) và (Đ’) bằng nhau.
Vậy tỉ số thể tích của (Đ) và (Đ’) bằng 1.



