Tổng số đo ba góc ngoài ở ba đình của tam giác là

Những câu hỏi liên quan
tổng số đo ba góc ngoài ở ba đỉnh của một tam giác
tổng số đo (độ) ba góc ngoài ở ba đỉnh của một tam giác
Chứng tỏ tổng số đo các góc ngoài ở ba đỉnh của một tam giác bằng 3600.
Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.
Ta có:
$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$
$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=540^0-180^0=360^0$
Đúng 2
Bình luận (0)
tổng số đo 3 góc ngoài ở ba đỉnh của một tam giác
3600, tớ nhớ câu này tớ làm r nek , bấm vào câu hỏi tươg tự xem thử coi có k
Đúng 0
Bình luận (0)
Cho tam giác ABC có A = 90 độ và B-C=20 độ
a. Tính số đo các góc và .
b. Chứng tỏ tổng số đo các góc ngoài ở ba đỉnh của một tam giác bằng 1800.
a. B = 55 độ
C = 35
b. lỗi. phải là 360 độ
ông họ ngô
tôi họ đinh
Đúng 4
Bình luận (0)
a) Cắt một tấm bìa hình tam giác và tô màu ba góc của nó (Hình 1a). Cắt rời ba góc ra khỏi tam giác rồi đặt ba góc kề nhau (Hình 1b).Em hãy dự đoán tổng số đo ba góc trong Hình 1b. b) Chứng minh tính chất về tổng số đo ba góc trong một tam giác theo gợi ý sau:GT Delta{ABC}KL widehat A+widehat B+widehat C {180^o}Qua A kẻ đường thẳng xy song song với BC như Hình 1c. Ta có: xy // BC Rightarrow widehat B ? (so le trong) (1) và widehat C ? (so le trong) (2)Từ (1)...
Đọc tiếp
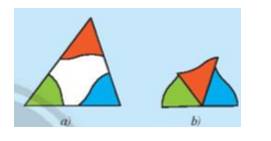
a) Cắt một tấm bìa hình tam giác và tô màu ba góc của nó (Hình 1a). Cắt rời ba góc ra khỏi tam giác rồi đặt ba góc kề nhau (Hình 1b).
Em hãy dự đoán tổng số đo ba góc trong Hình 1b.
b) Chứng minh tính chất về tổng số đo ba góc trong một tam giác theo gợi ý sau:
GT | \(\Delta{ABC}\) |
KL | \(\widehat A\)+\(\widehat B\)+\(\widehat C\)\( = {180^o}\) |
Qua A kẻ đường thẳng xy song song với BC như Hình 1c.
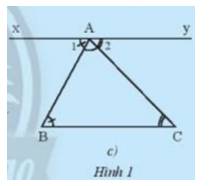
Ta có: xy // BC \( \Rightarrow \)\(\widehat B\)= ? (so le trong) (1)
và \(\widehat C\)= ? (so le trong) (2)
Từ (1) và (2) suy ra: \(\widehat B\)+\(\widehat {BAC}\)+\(\widehat C\)= \(\widehat {{A_1}}\)+\(\widehat {BAC}\)+\(\widehat {{A_2}}\)=\(\widehat {xAy}\)= ?
a) Ta dự đoán được sau khi ghép 3 góc nhọn đó sau khi ghép lại có tổng là \({180^o}\)
b) Qua A kẻ đường thẳng xy song song với BC
Ta có: xy // BC \( \Rightarrow \) \(\widehat B\) = \(\widehat {{A_1}}\) ( so le trong )
và \(\widehat C\) = \(\widehat {{A_2}}\)( so le trong )
Mà \(\widehat {{A_1}} + \widehat {BAC} + \widehat {{A_2}} = {180^o}\)
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \) Tổng 3 góc trong 1 tam giác = \({180^o}\)
Đúng 1
Bình luận (0)
Vẽ hai tam giác bất kì, dùng thước đo góc đo ba góc của mỗi tam giác rồi tính tổng số đo ba góc của mỗi tam giác.
Có nhận xét gì về các kết quả trên?
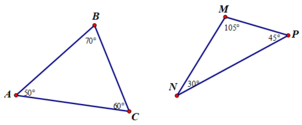
ΔABC có tổng ba góc là : 50o + 60o + 70o = 180o
ΔMNP có tổng ba góc là : 30o + 45o + 105o = 180o
Nhận xét: Tổng ba góc của hai tam giác đều là 1800
Đúng 0
Bình luận (0)
Định lí tổng ba góc trong một tam giác . Tính chất góc ngoài của tam giác.
+ ΔABC có Å+B+ACB = 180o(đ/l tổng ba góc trong một tam giác)
+Tính chất của ba góc ngoài
ACx=Å+B
Chứng minh rằng tổng ba góc ngoài ở ba đỉnh của một tam giác thì bằng 360º
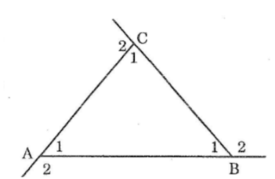
Ta có: ∠(A1 ) +∠(A2 ) =180o(hai góc kề bù)
∠(B1 ) +∠(B2 ) =180o(hai góc kề bù)
∠(C1 ) +∠(C2 )=180o(hai góc kề bù)
Suy ra: ∠(A1 ) +∠(A2 ) +∠(B1) +∠(B2 ) +∠(C1 ) +∠(C2 ) = 180º + 180º + 180º =540o
⇒∠(A2 ) + ∠( B2 ) +∠(C2 ) =540o-(∠(A1 ) +∠(B1 ) +∠(C1 ) ) (1)
Trong ΔABC, ta có:
∠(A1 ) +∠(B1 ) +∠(C1 ) =180o (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra: ∠(A2 ) +∠(B2 ) +∠(C2 ) =540o-180o=360o
Đúng 0
Bình luận (0)

















