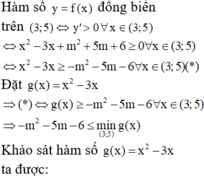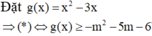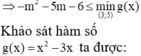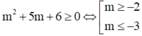Tìm giá trị của m để hàm số y=(2-m)x+5m đồng biến trên R

Những câu hỏi liên quan
Cho hàm số
y
m
+
5
m
-
5
.
x
+
2010
Tìm các giá trị của m để hàm số đã cho là hàm số bậc nhất đồng biến trê...
Đọc tiếp
Cho hàm số y = m + 5 m - 5 . x + 2010
Tìm các giá trị của m để hàm số đã cho là hàm số bậc nhất đồng biến trên R.
Với điều kiện m ≥ 0 và m ≠ 5 thì m + 5 > 0. Do đó, điều kiện để hàm số đã cho là hàm số bậc nhất đồng biến trên R là: m - 5 > 0, suy ra m > 5 ⇔ m > 5.
Đúng 0
Bình luận (0)
Tìm tập hợp các giá trị của tham số thực m để hàm số ymsinx+7x-5m+3 đồng biến trên R A.. B.. C.. D..
Đọc tiếp
Tìm tập hợp các giá trị của tham số thực m để hàm số y=msinx+7x-5m+3 đồng biến trên R
A.![]() .
.
B.![]() .
.
C.![]() .
.
D.![]() .
.
Chọn A
Ta có![]() .
.
![]() .
.
Hàm số ![]() đồng biến trên
đồng biến trên ![]() khi
khi ![]()
![]() .
.
Ta có ![]()
![]() .
.
+TH1 ![]()
![]()
![]()
![]() .
.
+TH2 ![]()
![]()
![]()
![]() .
.
Vậy ![]() .
.
Đúng 0
Bình luận (0)
bài1cho hàm số Y(2-m)x-2tìm các giá trị của m để HS bậc nhất.tìm hệ số a,bbài 2, cho hàm số Y(m-5)x+1.tìm các giá trị để hàm sốa, đồng biến trên R b,nghịch biến trên Rbài 3,cho 2 HS bậc nhất Y(3-m)timesx+2(d1) và Y2x+m(d2)a,tìm giá trị của m để đồ thị hai hàm số song song với nhaub,tìm giá trị của m để đồ thị hai hàm số cắt nhauc,tìm giá trị của m để đồ thị hai hàm số cắt nhau tại 1 điểm trên trục tungbài 4, cho HS Y2x1.tìm hệ số góc ,tung độ gốc,vẽ đồ thị HS...
Đọc tiếp
bài1cho hàm số Y=(2-m)x-2tìm các giá trị của m để HS bậc nhất.tìm hệ số a,b
bài 2, cho hàm số Y=(m-5)x+1.tìm các giá trị để hàm số
a, đồng biến trên R b,nghịch biến trên R
bài 3,cho 2 HS bậc nhất Y=(3-m)\(\times\)x+2(d1) và Y=2x+m(d2)
a,tìm giá trị của m để đồ thị hai hàm số song song với nhau
b,tìm giá trị của m để đồ thị hai hàm số cắt nhau
c,tìm giá trị của m để đồ thị hai hàm số cắt nhau tại 1 điểm trên trục tung
bài 4, cho HS Y=2x=1.tìm hệ số góc ,tung độ gốc,vẽ đồ thị HS trên ,tính góc tạo bởi đường thẳng trên với trục ox
Bài 1:
Để hàm số y=(2-m)x-2 là hàm số bậc nhất thì 2-m<>0
=>m<>2
a=2-m
b=-2
Bài 2:
a: Để hàm số y=(m-5)x+1 đồng biến trên R thì m-5>0
=>m>5
b: Để hàm số y=(m-5)x+1 nghịch biến trên R thì m-5<0
=>m<5
Bài 3:
a: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}3-m=2\\2\ne m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=1\)
b: Để (d1) cắt (d2) thì \(3-m\ne2\)
=>\(m\ne1\)
c: Để (d1) cắt (d2) tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}3-m\ne2\\m=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne1\\m=2\end{matrix}\right.\)
=>m=2
Đúng 0
Bình luận (0)
Tìm giá trị của M để hàm số y=5-m^2/4-m^2 nhan với x+1 để hàm số đồng biến và nghịch biến trên R
Cho hàm số yf(x) có đạo hàm
y
x
2
-
3
x
+
m
2
+
5
m
+
6
. Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5) A. B. C. D. Với mọi
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm y ' = x 2 - 3 x + m 2 + 5 m + 6 . Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5)
A. ![]()
B.![]()
C. ![]()
D. Với mọi ![]()
Cho hàm số y f(x) có đạo hàm
y
x
2
-
3
x
+
m
2
+
5
m
+
6
. Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5)
Đọc tiếp
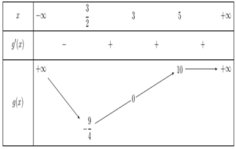
Cho hàm số y = f(x) có đạo hàm y ' = x 2 - 3 x + m 2 + 5 m + 6 . Tìm tất cả các giá trị của m để hàm số đồng biến trên (3;5)
![]()
![]()
![]()
![]()
Tìm các giá trị của m để hàm số y=1/3(m-1) x^3-(m-1)x^2 + x + 2 đồng biến trên R
y'=1/3*3x^2(m-1)-(m-1)2x+1
=x^2(m-1)-x(2m-2)+1
Để hàm số đồng biến trên R thì y'>0 với mọi x
=>m-1<>0 và (2m-2)^2-4(m-1)>0
=>m<>1 và 4m^2-8m+4-4m+4>0
=>4m^2-12m+8>0 và m<>1
=>m^2-3m+2>0 và m<>1
=>m>2 hoặc m<1
Đúng 0
Bình luận (0)
Tìm giá trị của m để hàm số y x + m(sinx + cosx + m ) luôn đồng biến trên R A.
-
2
2
≤
m
≤
2
2
B.
0
≤
m
≤
2
2
C.
-
2
2
≤
m
≤
0...
Đọc tiếp
Tìm giá trị của m để hàm số y = x + m(sinx + cosx + m ) luôn đồng biến trên R
A. - 2 2 ≤ m ≤ 2 2
B. 0 ≤ m ≤ 2 2
C. - 2 2 ≤ m ≤ 0
D. - 2 ≤ m ≤ 2
y ' = 1 + m cos x - sin x = 1 - 2 m sin x - π 4
Đặt t = sin x - π 4 với t ∈ - 1 ; 1 ta có f 1 = 1 - 2 m t
Để hàm số đồng biến trên R thì
f t ≥ 0 ∀ t ∈ - 1 ; 1 ⇔ f - 1 ≥ 0 f 1 ≥ 0 ⇔ 1 + 2 m ≥ 0 1 - 2 m ≥ 0
⇔ m ≥ - 2 2 m ≤ 2 2 ⇔ - 2 2 ≤ m ≤ 2 2
Đáp án A
Đúng 0
Bình luận (0)
Tìm các giá trị của m để hàm số y (
m
2
− m)x + 1 đồng biến trên R. A. 0 m 1 B. m
∈
(
−
∞
;
0
)
∪
(
1
;
+
∞
)
C.
m
0
m...
Đọc tiếp
Tìm các giá trị của m để hàm số y = ( m 2 − m)x + 1 đồng biến trên R.
A. 0 < m < 1
B. m ∈ ( − ∞ ; 0 ) ∪ ( 1 ; + ∞ )
C. m = 0 m = 1
D. Không tồn tại
Tìm giá trị nhỏ nhất của m làm cho hàm số
y
1
3
x
3
+
m
x
2
-
m
x
-
m
2
+
5
m
đồng biến trên R A. -4 B. -1 C. 0 D. 1
Đọc tiếp
Tìm giá trị nhỏ nhất của m làm cho hàm số
y = 1 3 x 3 + m x 2 - m x - m 2 + 5 m
đồng biến trên R
A. -4
B. -1
C. 0
D. 1
Hàm số đồng biến trên R
⇔ y ' = x 2 + 2 m x - m ≥ 0 ⇔ ∆ ' = m 2 + m ≤ 0 ⇔ - 1 ≤ m ≤ 0
Suy ra giá trị nhỏ nhất của m là -1
Đáp án B
Đúng 0
Bình luận (0)